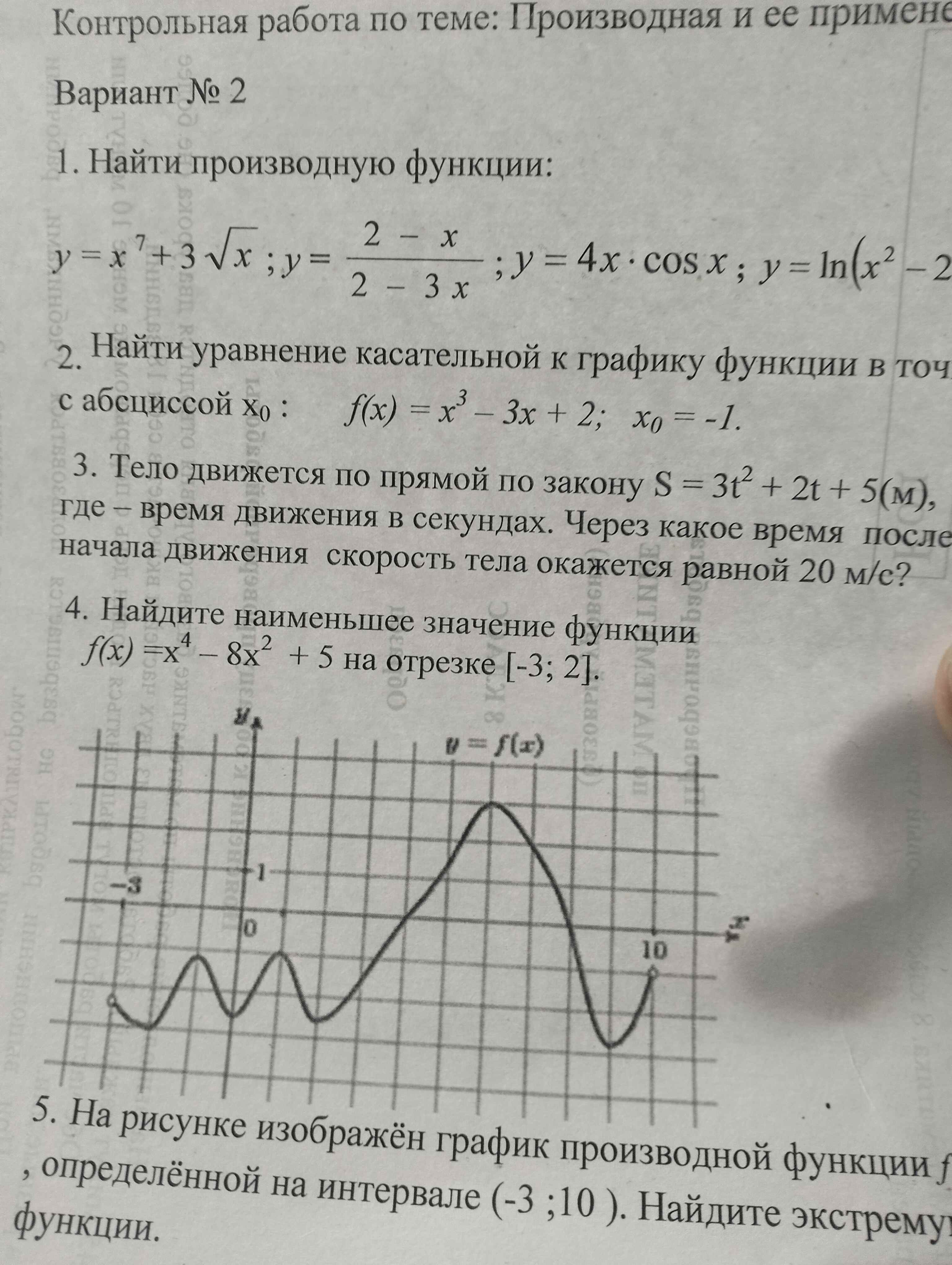
1. Найти производную функции: $y=x^7+3\sqrt{x}$; $y=\frac{2-x}{2-3x}$; $y=4x \cdot cos x$; $y=ln(x^2-2x)$

Решение: 1. $y=x^7+3\sqrt{x} = x^7 + 3x^{\frac{1}{2}}$ $y' = (x^7)' + (3x^{\frac{1}{2}})' = 7x^6 + 3 \cdot \frac{1}{2} x^{-\frac{1}{2}} = 7x^6 + \frac{3}{2\sqrt{x}}$ Ответ: $y' = 7x^6 + \frac{3}{2\sqrt{x}}$ 2. $y=\frac{2-x}{2-3x}$ $y' = \frac{(2-x)'(2-3x) - (2-x)(2-3x)'}{(2-3x)^2} = \frac{(-1)(2-3x) - (2-x)(-3)}{(2-3x)^2} = \frac{-2+3x+6-3x}{(2-3x)^2} = \frac{4}{(2-3x)^2}$ Ответ: $y' = \frac{4}{(2-3x)^2}$ 3. $y = 4x \cdot cos x$ $y' = (4x)' \cdot cos x + 4x \cdot (cos x)' = 4 \cdot cos x + 4x \cdot (-sin x) = 4cos x - 4xsin x$ Ответ: $y' = 4cos x - 4xsin x$ 4. $y = ln(x^2 - 2x)$ $y' = \frac{1}{x^2-2x} \cdot (x^2-2x)' = \frac{2x-2}{x^2-2x} = \frac{2(x-1)}{x(x-2)}$ Ответ: $y' = \frac{2(x-1)}{x(x-2)}$