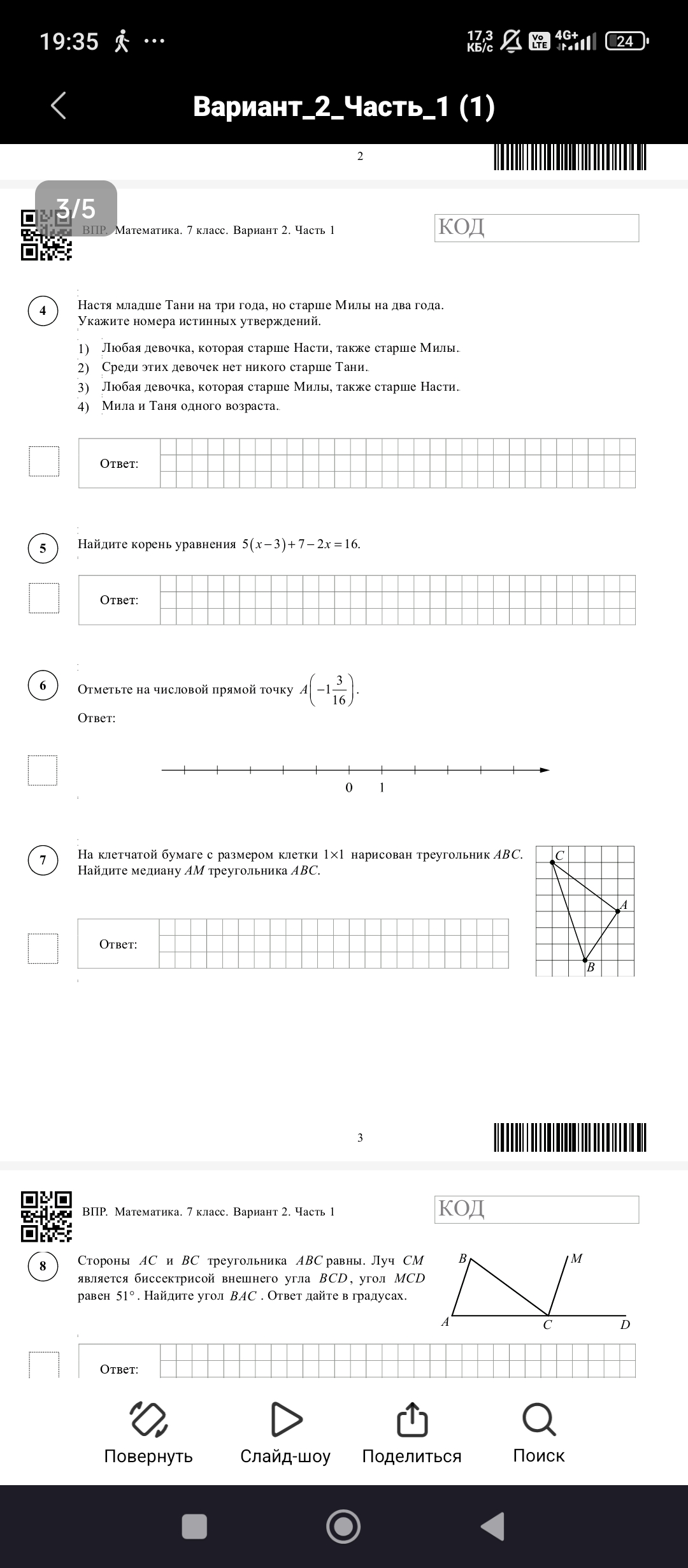
8. Стороны $AC$ и $BC$ треугольника $ABC$ равны. Луч $CM$ является биссектрисой внешнего угла $BCD$, угол $MCD$ равен 51°. Найдите угол $BAC$. Ответ дайте в градусах.

1. Так как $CM$ - биссектриса внешнего угла $BCD$, то $\angle BCM = \angle MCD = 51^\circ$. 2. Тогда $\angle BCD = \angle BCM + \angle MCD = 51^\circ + 51^\circ = 102^\circ$. 3. Угол $ACB$ является смежным с углом $BCD$, поэтому $\angle ACB = 180^\circ - \angle BCD = 180^\circ - 102^\circ = 78^\circ$. 4. Так как стороны $AC$ и $BC$ треугольника $ABC$ равны, то треугольник $ABC$ является равнобедренным с основанием $AB$. Следовательно, углы при основании равны: $\angle BAC = \angle ABC$. 5. Сумма углов в треугольнике равна 180°. Поэтому $\angle BAC + \angle ABC + \angle ACB = 180^\circ$. Так как $\angle BAC = \angle ABC$, можно записать $2 \cdot \angle BAC + \angle ACB = 180^\circ$. 6. Подставим значение $\angle ACB = 78^\circ$: $2 \cdot \angle BAC + 78^\circ = 180^\circ$. 7. Выразим $\angle BAC$: $2 \cdot \angle BAC = 180^\circ - 78^\circ = 102^\circ$. 8. Разделим на 2: $\angle BAC = \frac{102^\circ}{2} = 51^\circ$. Ответ: 51