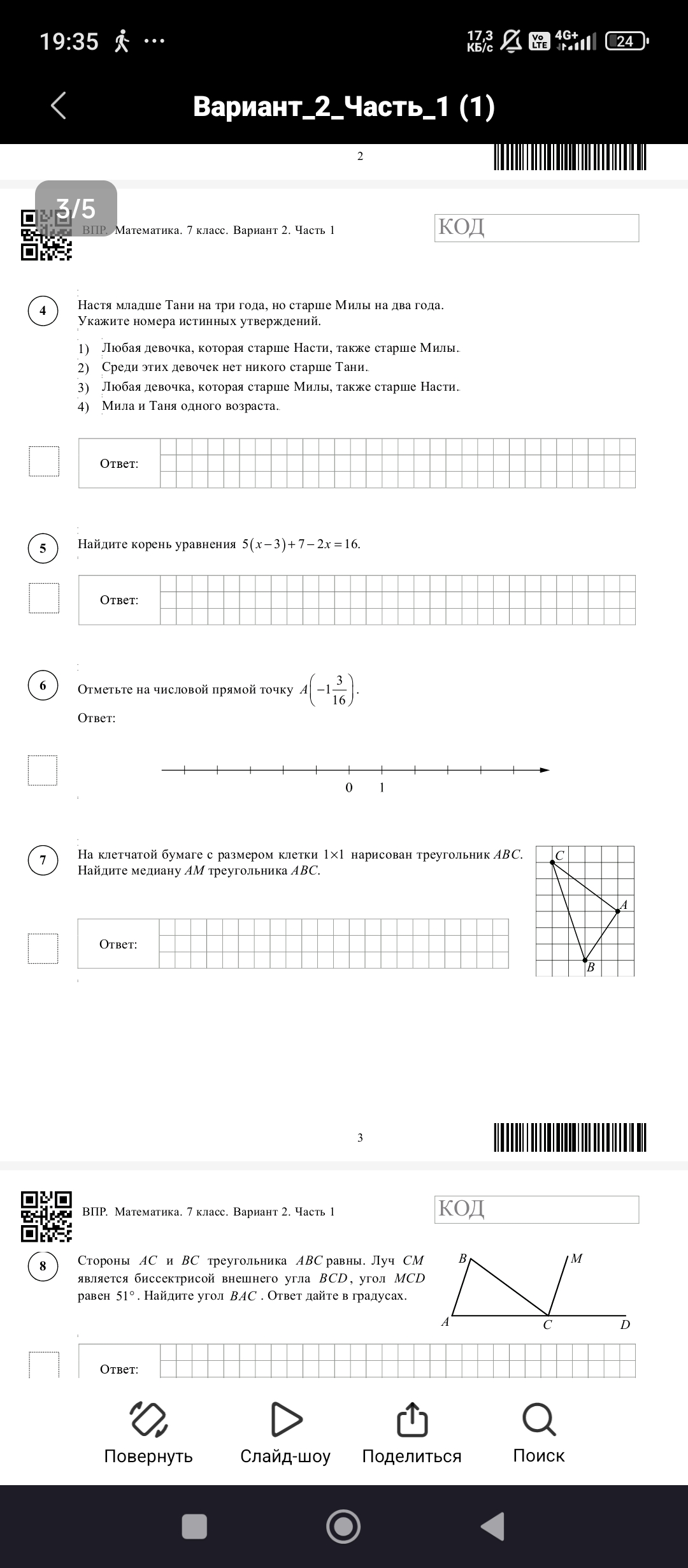
4. Настя младше Тани на три года, но старше Милы на два года. Укажите номера истинных утверждений. 1) Любая девочка, которая старше Насти, также старше Милы. 2) Среди этих девочек нет никого старше Тани. 3) Любая девочка, которая старше Милы, также старше Насти. 4) Мила и Таня одного возраста.

Обозначим возраст Насти как $$N$$, возраст Тани как $$T$$, а возраст Милы как $$M$$. Из условия задачи мы знаем: $$N = T - 3$$ (Настя младше Тани на три года) $$N = M + 2$$ (Настя старше Милы на два года) Выразим возраст Тани и Милы через возраст Насти: $$T = N + 3$$ $$M = N - 2$$ Теперь рассмотрим каждое утверждение: 1) Любая девочка, которая старше Насти, также старше Милы. Это верно, потому что $$T = N + 3$$, и, следовательно, Таня старше Насти. И так как $$M = N - 2$$, Настя всегда будет старше Милы. Следовательно, Таня тоже старше Милы. 2) Среди этих девочек нет никого старше Тани. Это неверно, так как мы определили, что $$T = N + 3$$, то есть Таня старше Насти. 3) Любая девочка, которая старше Милы, также старше Насти. Это неверно, потому что Настя старше Милы, но при этом сама Мила младше Насти. 4) Мила и Таня одного возраста. Это неверно, так как $$M = N - 2$$ и $$T = N + 3$$, следовательно, $$T
eq M$$. Таким образом, только утверждение 1 верно. Ответ: 1