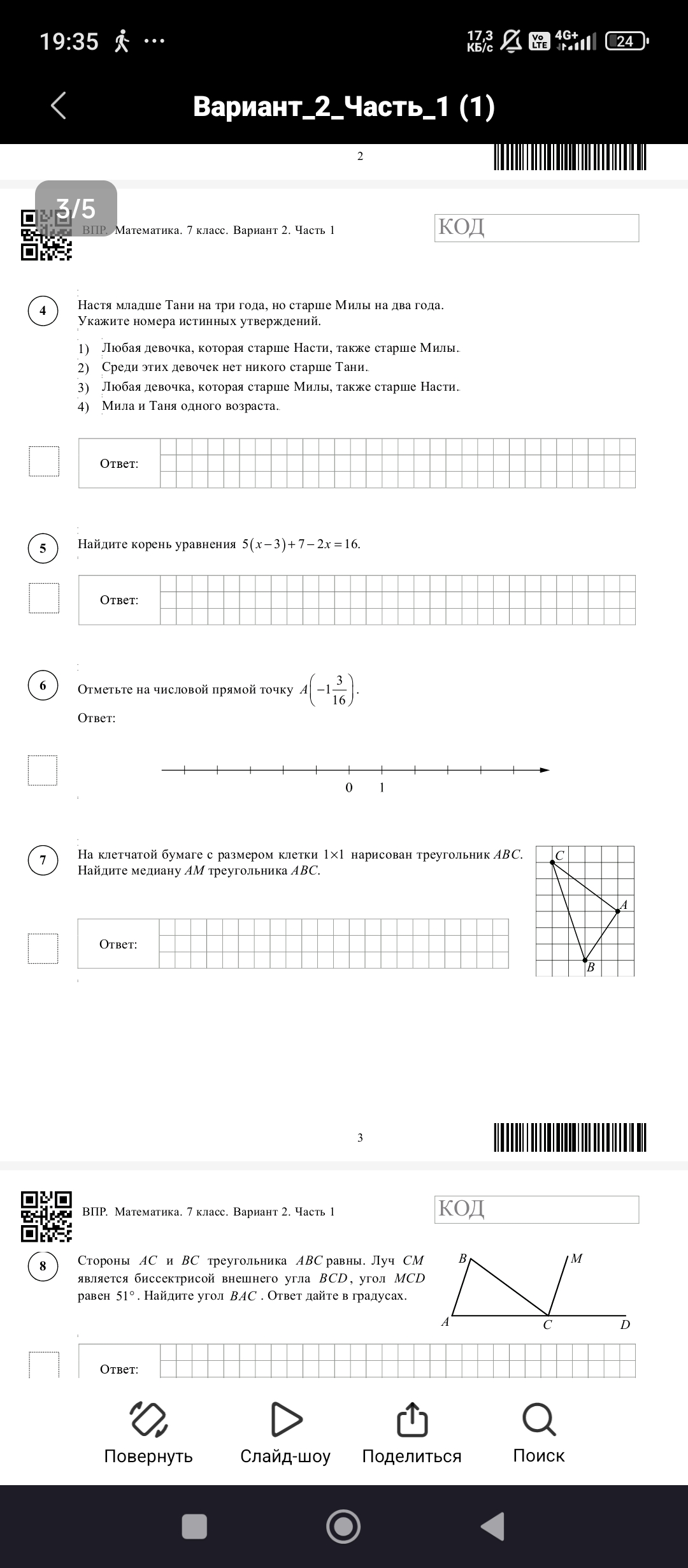
7. На клетчатой бумаге с размером клетки 1×1 нарисован треугольник $ABC$. Найдите медиану $AM$ треугольника $ABC$.

Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В данном случае нам нужно найти медиану $AM$, где $M$ - середина стороны $BC$. 1. Определим координаты точек: $A(5, 6)$, $B(2, 2)$, $C(8, 8)$. 2. Найдем координаты точки $M$ как середины отрезка $BC$: $M(\frac{2+8}{2}, \frac{2+8}{2}) = M(5, 5)$. 3. Найдем длину медианы $AM$ по формуле расстояния между двумя точками: $AM = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} = \sqrt{(5 - 5)^2 + (5 - 6)^2} = \sqrt{0^2 + (-1)^2} = \sqrt{1} = 1$. Ответ: 1