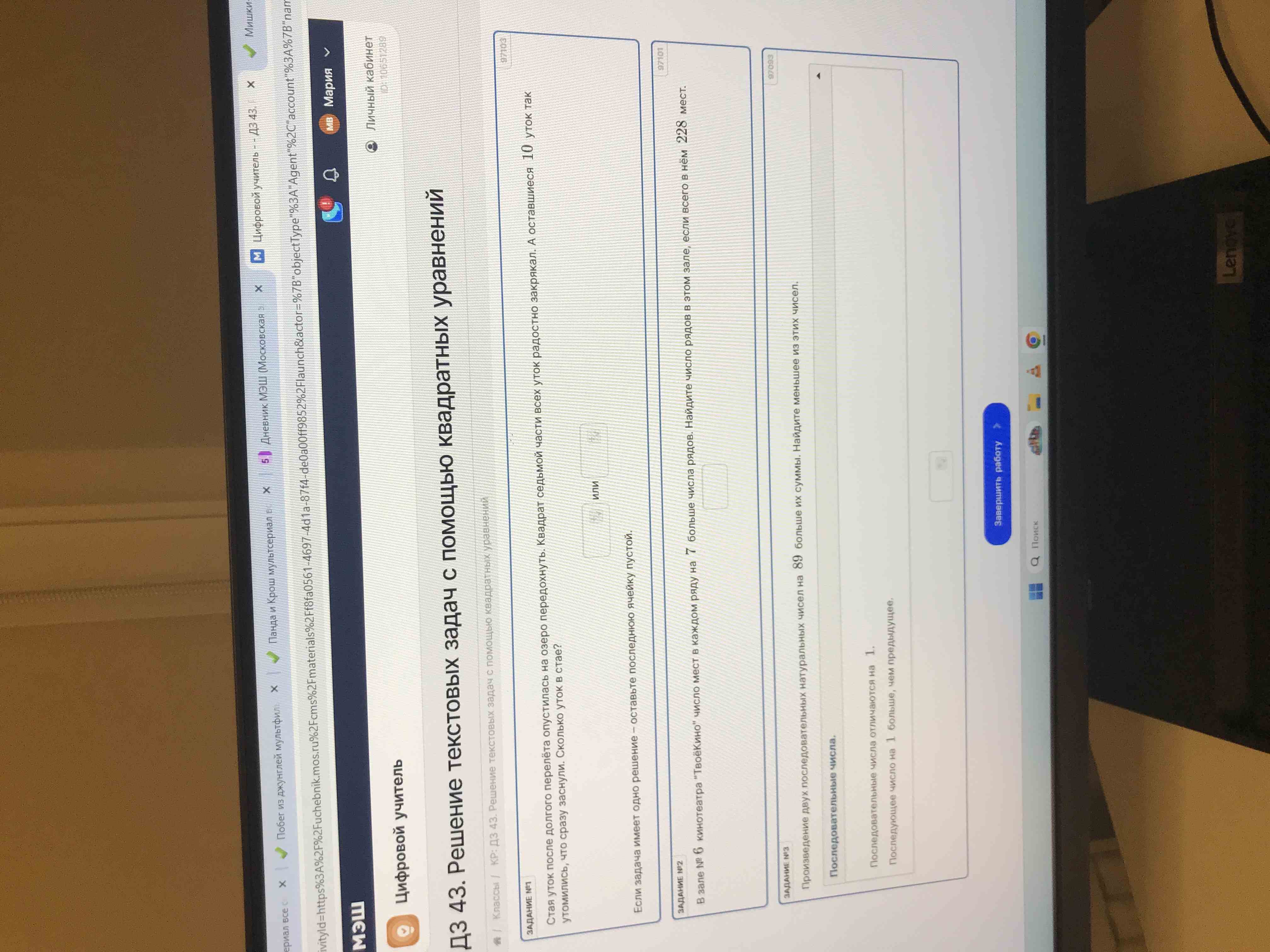
ЗАДАНИЕ №2: В зале № 6 кинотеатра "ТвоёКино" число мест в каждом ряду на 7 больше числа рядов. Найдите число рядов в этом зале, если всего в нём 228 мест.

Пусть \( x \) - число рядов в зале. Тогда количество мест в каждом ряду будет \( x + 7 \). Общее количество мест в зале равно произведению количества рядов на количество мест в ряду, то есть \( x(x + 7) \). По условию, общее количество мест равно 228. Составим уравнение: \( x(x + 7) = 228 \) Раскроем скобки: \( x^2 + 7x = 228 \) Перенесём всё в одну сторону и получим квадратное уравнение: \( x^2 + 7x - 228 = 0 \) Решим квадратное уравнение через дискриминант: \( D = b^2 - 4ac = 7^2 - 4 * 1 * (-228) = 49 + 912 = 961 \) \( \sqrt{D} = \sqrt{961} = 31 \) Теперь найдём корни уравнения: \( x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-7 + 31}{2} = \frac{24}{2} = 12 \) \( x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-7 - 31}{2} = \frac{-38}{2} = -19 \) Так как количество рядов не может быть отрицательным, выбираем положительный корень \( x = 12 \). Следовательно, число рядов в зале - 12. Ответ: 12.