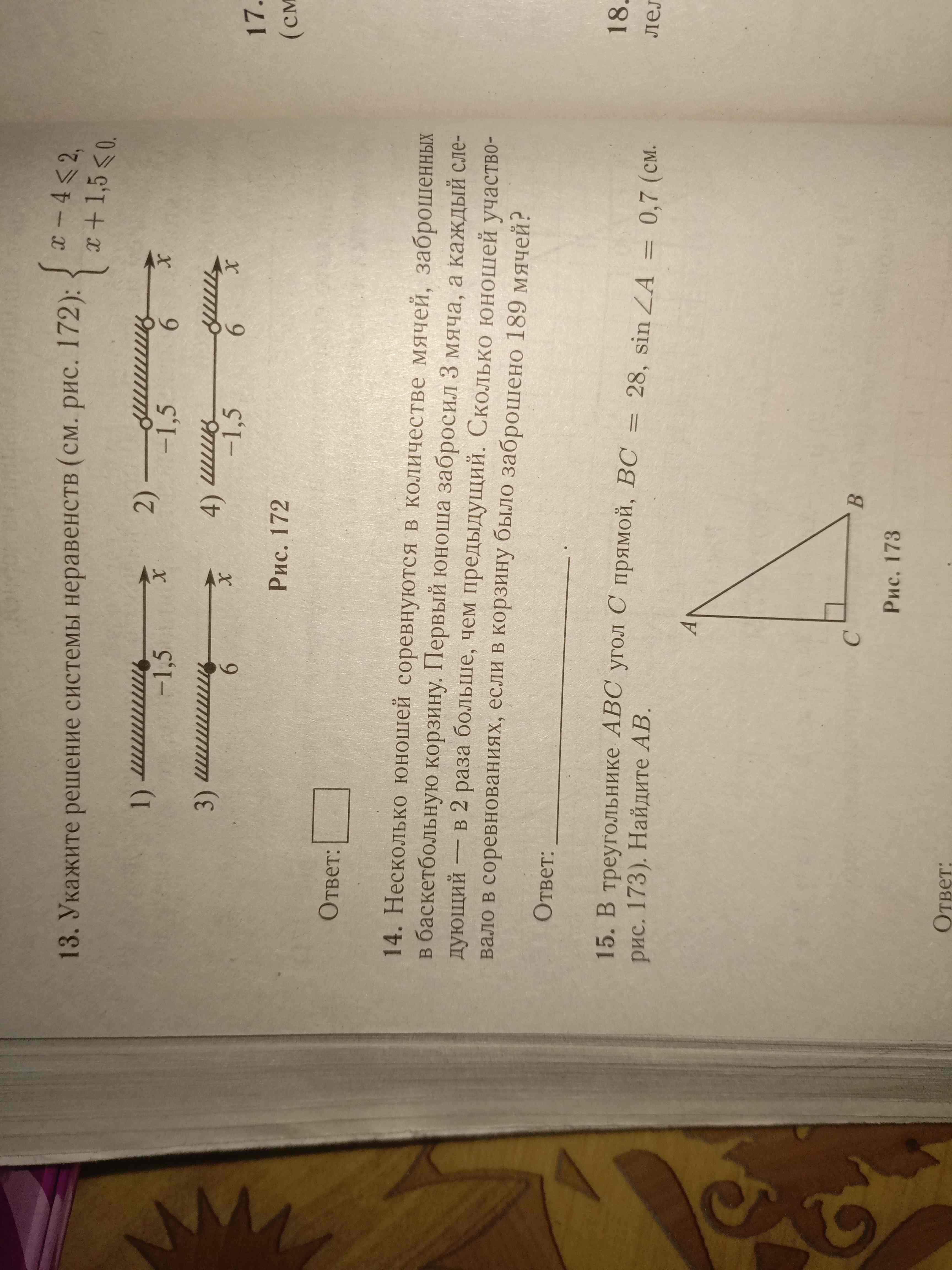
13. Укажите решение системы неравенств (см. рис. 172): $\begin{cases} x - 4 \le 2, \\ x + 1,5 \le 0. \end{cases}$

Для решения системы неравенств необходимо решить каждое неравенство по отдельности и найти пересечение полученных решений. 1. Решим первое неравенство: $x - 4 \le 2$. Добавим 4 к обеим частям неравенства: $x \le 6$. 2. Решим второе неравенство: $x + 1,5 \le 0$. Вычтем 1,5 из обеих частей неравенства: $x \le -1,5$. Теперь найдем пересечение решений. На числовой прямой это область, где $x \le -1,5$ и $x \le 6$. Так как $-1,5 < 6$, пересечением будет область $x \le -1,5$. Таким образом, решением системы неравенств является $x \le -1,5$. На рисунке 172 необходимо найти график, который соответствует решению $x \le -1,5$. Это график номер 1. **Ответ: 1**