Теплоход проходит 60 км против течения реки и 54 км в стоячей воде за 4 ч 30 мин. На прохождение 162 км в стоячей воде теплоходу требуется на 3 ч больше, чем на прохождение 72 км против течения этой реки. Найдите собственную скорость теплохода и скорость течения реки.

\[Пусть\ x\ \frac{км}{ч} - скорость\ \]

\[І\ поезда;\]

\[а\ y\ \frac{км}{ч} - скорость\ ІІ\ поезда.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} - \frac{90}{x} + \frac{90}{y} = 1\frac{15}{60} \\ 3y - x = 30\ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} \frac{90}{y} - \frac{90}{x} - \frac{5}{4} = 0 \\ x = 3y - 30\ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\frac{90}{y} - \frac{90}{3y - 30} - \frac{5}{4} = 0\]

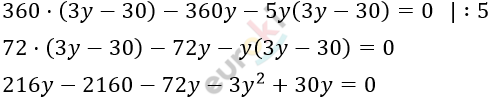
\[3y² - 174y + 2160 = 0\ \ \ |\ :3\]

\[y^{2} - 58y + 720 = 0\]

\[D = 3364 - 2880 = 484 = 22^{2}\]

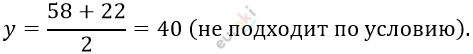
\[y = \frac{58 - 22}{2} = 18\ \left( \frac{км}{ч} \right) -\]

\[скорость\ одного\ катера.\]

\[3 \cdot 18 - 30 = 24\ \left( \frac{км}{ч} \right) -\]

\[скорость\ \ другого\ катера.\]

\[Ответ:18\frac{км}{ч};24\frac{км}{ч}.\]