От пристани A в направлении пристани B, расстояние между которыми равно 90 км, отправились одновременно два катера. Первый катер прибыл на пристань B на 1 ч 15 мин раньше второго. Найдите скорость каждого катера, если второй катет за 3 ч проходит на 30 км больше, чем первый за 1 час, и скорость каждого катера не превышает 30 км/ч.

Ответ:

\[Пусть\ x\ \frac{км}{ч} - скорость\ \]

\[одного\ велосипедиста,\ \]

\[а\ y\ \frac{км}{ч} - скорость\ другого\ \]

\[велосипедиста.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} 2 \cdot (x + y) = 50\ \ |\ :2 \\ \frac{50}{x} - \frac{50}{y} = 1\frac{40}{60}\text{\ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} x + y = 25\ \ \ \\ \frac{50}{x} - \frac{50}{y} = \frac{5}{3} \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]

\[\left\{ \begin{matrix} x = 25 - y\ \ \ \ \ \ \ \ \ \ \ \\ \frac{50}{25 - y} - \frac{50}{y} = \frac{5}{3} \\ \end{matrix} \right.\ ,\ y \neq 25\]

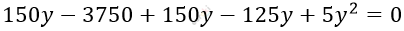
\[5y² + 175y - 3750 = 0\ \ \ |\ :5\]

\[y^{2} + 35y - 750 = 0\]

\[D = 1225 + 3000 = 4225 = 65^{2}\]

\[y = \frac{- 35 - 65}{2} < 0;\ \ \]

\[y = \frac{- 35 + 65}{2} = 15\ \left( \frac{км}{ч} \right) -\]

\[скорость\ одного\ \]

\[велосипедиста.\]

\[25 - 15 = 10\ \left( \frac{км}{ч} \right) -\]

\[скорость\ другого.\]

\[Ответ:15\ \frac{км}{ч};10\ \frac{км}{ч}.\]