Две бригады, работая одновременно, могут отремонтировать дорогу за 6 ч. Если же сначала первая бригада самостоятельно отремонтирует 3/5 дороги, а потом вторая – оставшуюся часть дороги, то весь ремонт будет выполнен за 12 ч. За сколько часов может отремонтировать дорогу каждая бригада, работая самостоятельно?

Ответ:

\[Пусть\ скорости\ автомобилей\ \]

\[\text{x\ }\frac{км}{ч}\ и\ \ y\ \frac{км}{ч},\ так\ как\ они\]

\[встретились\ на\ середине\ пути,\ \]

\[то\ 240\ :2 = 120\ км.\]

\[2\ ч\ 24\ мин = 2\frac{2}{5} = \frac{12}{5}\ ч.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} \frac{12}{5} \cdot (x + y) = 240 \\ \frac{120}{x} - \frac{120}{y} = 1\ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} x + y = 100\ \ \ \ \ \ \ \ \ \ \ \ \\ \frac{120}{x} - \frac{120}{y} - 1 = 0 \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]

\[\left\{ \begin{matrix} x = 100 - y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \frac{120}{100 - y} - \frac{120}{y} - 1 = 0 \\ \end{matrix} \right.\ \]

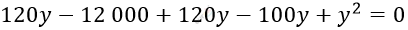
\[y^{2} + 140y - 12\ 000 = 0\]

\[D = 19\ 600 + 48\ 000 =\]

\[= 67\ 600 = 260^{2}\]

\[y = \frac{- 140 - 260}{2} < 0.\ \ \]

\[y = \frac{- 140 + 260}{2} = 60\ \left( \frac{км}{ч} \right) -\]

\[скорость\ одного\ автомобиля.\]

\[100 - 60 = 40\ \left( \frac{км}{ч} \right) -\]

\[скорость\ другого\ \]

\[автомобиля.\]

\[Ответ:60\ \frac{км}{ч};40\ \frac{км}{ч}.\]