Вопрос:
Пусть х1 и х2 – корни квадратного уравнения 3х2 – 4x – 2 = 0. Составьте квадратное уравнение, корнями которого являются числа 2/х1 и 2/х2.
Ответ:
\[3x^{2} - 4x - 2 = 0\]
\[x^{2} - \frac{4}{3x} - \frac{2}{3} = 0\]
\[x_{1} + x_{2} = \frac{4}{3};\ \ \ \ \ \ \ \ x_{1}x_{2} = - \frac{2}{3}\]
\[\frac{2}{x_{1}} + \frac{2}{x_{2}} = \frac{2x_{1} + 2x_{2}\ }{x_{1}x_{2}} =\]
\[= \frac{2 \cdot \left( x_{1} + x_{2} \right)}{x_{1}x_{2}} = \frac{2 \cdot \frac{4}{3}}{- \frac{2}{3}} =\]
\[= - \frac{2 \cdot 4 \cdot 3}{3 \cdot 2} = - 4.\]
\[\frac{2}{x_{1}} \cdot \frac{2}{x_{2}} = \frac{4}{x_{1}x_{2}} = \frac{4}{- \frac{2}{3}} = - \frac{4 \cdot 3}{2} =\]
\[= - 6.\]
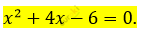
Похожие
- Несколько одноклассников организовали турнир по шашкам. Каждый участник турнира сыграл с каждым по одной партии. За выигрыш присуждали 2 очка, за ничью – 1 очко, за проигрыш – 0 очков. Пять самых слабых игроков набрали вместе 26 очков – в 5 раз меньше, чем остальные участники, вместе взятые. Сколько было участников турнира?
- Решите уравнение: (2x^2-5x-7)(x-1)=0.
- Уравнение x2 – 7x + q = 0 имеет корень –3. Найдите его второй корень и число q.