При каждом значении параметра a решите уравнение: a^2 x-2a=4*(x-1).

\[a^{2}x - 2a = 4 \bullet (x - 1)\]

\[a^{2}x - 2a = 4x - 4\]

\[a^{2}x - 4x = 2a - 4\]

\[x\left( a^{2} - 4 \right) = 2 \bullet (a - 2)\]

\[x(a - 2)(a + 2) = 2 \bullet (a - 2)\]

\[a = - 2 \Longrightarrow нет\ решения.\]

\[a = 2 \Longrightarrow x - любое.\]

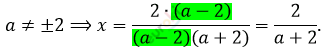
\[Ответ:нет\ решения\ при\ \]

\[a = - 2;\ \ \]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ x - любое\ при\ a = 2;\]

\[\ \ \ \ \ \ \ \ \ \ \ x = \frac{2}{a + 2}\ при\ a \neq \pm 2.\]