Вопрос:

Построив в одной системе координат графики функций y=12/x и y=-x^2-3x+4. Определите, пользуясь определённым рисунком, количество корней уравнения –x^2-3x+4=12/x.

Ответ:

\[y = \frac{12}{x}\]

\[x\]	\[\pm 3\]	\[\pm 4\]
\[y\]	\[\pm 4\]	\[\pm 3\]

\[y = - x^{2} - 3x + 4\]

\[x_{0} = - \frac{3}{2};\ \ \ \]

\[y_{0} = - \frac{9}{4} + \frac{9}{2} + 4 = 6\frac{1}{4}\]

\[x\]	\[0\]	\[1\]
\[y\]	\[4\]	\[0\]

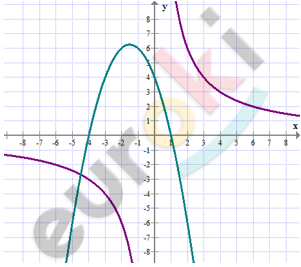
\[Ответ:1\ решение.\]

Похожие

Поставьте вместо многоточия такой из знаков>, <, >=, <=, при котором получившееся неравенство будет верным при любых значениях x и y: –x^2…0.
Постойте график функции y=x^2+2x-3. При каком значении аргумента функция достигает своего наименьшего значения? Чему равно это значение?
Постойте график функции y=x^2+6x. При каком значении аргумента функция достигает своего наименьшего значения? Чему равно это значение?
Постойте график функции y=x^2-2x-3. При каком значении аргумента функция достигает своего наименьшего значения? Чему равно это значение?
Постойте график функции y=x^2-6x. При каком значении аргумента функция достигает своего наименьшего значения? Чему равно это значение?
Построив в одной системе координат графики функций y=12/x и y=-x^2-x+6, определите количество корней уравнения –x^2-x+6=12/x.
Построив в одной системе координат графики функций y=8/x и y=-x^2+6x-5, определите количество корней уравнения –x^2+6x-5=8/x.
Построить в координатной плоскости треугольник ABM, если A (2;-5); B (1; 4); M (-6; 3).
Построить в координатной плоскости треугольник MKP, если M (-6; 3); K (-2;3); P(6; 9).
Построить график функции f(x)=(x+1)^2 при x<0; 1-x^2 при x>=0.