Пассажирский поезд должен пройти с постоянной скоростью расстояние между станциями, равное 448 км. Когда он прошел половину этого расстояния, то был задержан у светофора на 24 мин, поэтому, чтобы наверстать опоздание, машинист увеличил скорость поезда на оставшемся участке пути на 10 км/ч. С какой скоростью поезд шел после остановки?

\[24\ мин = \frac{2}{5}\ ч.\]

\[448\ :2 = 224\ (км) -\]

\[половина\ пути.\]

\[Составим\ уравнение:\ \]

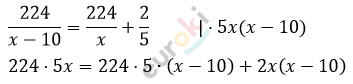
\[1120x =\]

\[= 1120x - 11200 + 2x^{2} - 20x\]

\[2x^{2} - 20x - 11200 = 0\ \ \ \ \ \ \ \ |\ :2\]

\[x^{2} - 10x - 5600 = 0\]

\[D = ( - 10)^{2} - 4 \cdot 1 \cdot ( - 5600) =\]

\[= 100 + 22400 = 22500\]

\[x_{1} = \frac{10 + \sqrt{22500}}{2} = \frac{10 + 150}{2} =\]

\[= \frac{160}{2} = 80\ \left( \frac{км}{ч} \right) - скорость\ \]

\[поезда\ после\ остановки.\]

\[x_{2} = \frac{10 - \sqrt{22500}}{2} =\]

\[= \frac{10 - 150}{2} = \frac{- 140}{2} =\]

\[= - 70\ (не\ подходит).\]

\[Ответ:80\ \frac{км}{ч.}\]