Два туриста, сменяясь, перенесли рюкзак на расстояние 11 км. При этом каждый нес рюкзак по одному часу. Какова скорость второго туриста, если 3 км он проходил на 6 мин медленнее, чем первый турист проходил 2 км?

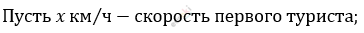
\[x\ км - прошел\ первый\ турист\ \]

\[за\ 1\ ч.\]

\[(11 - x)\ км - прошел\ второй\ \]

\[за\ 1\ ч;\]

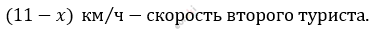
\[60\ мин = \frac{1}{10}\ ч.\]

\[Составим\ уравнение:\]

\[\frac{3}{11 - x} - \frac{2}{x} = \frac{1}{10}\]

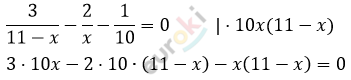
\[30x - 220 + 20x - 11x + x^{2} =\]

\[= 0\]

\[x^{2} + 39x - 220 = 0\]

\[D = 39^{2} - 4 \cdot 1 \cdot ( - 220) =\]

\[= 1521 + 880 = 2401\]

\[x_{1} = \frac{- 39 + \sqrt{2401}}{2} =\]

\[= \frac{- 39 + 49}{2} = \frac{10}{2} = 5\ \left( \frac{км}{ч} \right) -\]

\[скорость\ первого\ туриста.\]

\[x_{2} = \frac{- 39 - \sqrt{2401}}{2} =\]

\[= \frac{- 39 - 49}{2} = \frac{- 88}{2} =\]

\[= - 44\ \ (не\ подходит).\]

\[11 - x = 11 - 5 = 6\ \left( \frac{км}{ч} \right) -\]

\[скорость\ второго\ туриста.\]

\[Ответ:6\ \frac{км}{ч.}\]