Пассажирский поезд должен пройти с постоянной скоростью расстояние между станциями, равное 312 км. Когда он прошел половину этого расстояния, то был задержан у светофора на 12 мин, поэтому, чтобы наверстать опоздание, машинист увеличил скорость поезда на оставшемся участке пути на 5 км/ч. С какой скоростью поезд шел после остановки?

\[312\ :2 = 156\ (км) - половина\ \]

\[пути.\]

\[Составим\ уравнение:\]

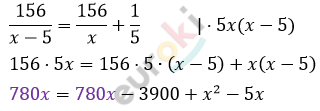
\[x^{2} - 5x - 3900 = 0\]

\[D = ( - 5)^{2} - 4 \cdot 1 \cdot ( - 3900) =\]

\[= 25 + 15600 = 15625\]

\[x_{1} = \frac{5 + \sqrt{15625}}{2} = \frac{5 + 125}{2} =\]

\[= \frac{130}{2} = 65\ \left( \frac{км}{ч} \right) - скорость\ \]

\[поезда\ после\ остановки.\]

\[x_{2} = \frac{5 - \sqrt{15625}}{2} = \frac{5 - 125}{2} =\]

\[= \frac{- 120}{2} = - 60\ (не\ подходит).\]

\[Ответ:65\ \frac{км}{ч.}\]