Две трубы наполнили бассейн объемом 17 м³. При этом первая труба была открыта 2 ч, а вторая 3 ч. Сколько кубометров заполнила первая труба, если 1 м³ она заполняла на 5 мин быстрее, чем вторая?

\[2\ ч = 120\ мин;\ \ \ 3\ ч = 180\ мин.\]

\[Составим\ уравнение:\]

\[120 \cdot \frac{1}{x} + \frac{1}{x + 5} \cdot 180 = 17\]

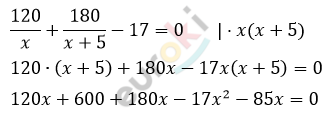
\[17x^{2} + 215x + 600 = 0\]

\[17x^{2} - 215x - 600 = 0\]

\[D = ( - 215)^{2} - 4 \cdot 17 \cdot ( - 600) =\]

\[= 46225 + 40800 = 87025\]

\[x_{1} = \frac{215 + \sqrt{87025}}{2 \cdot 17} =\]

\[= \frac{215 + 295}{34} = \frac{510}{34} = 15\]

\[x_{2} = \frac{215 - \sqrt{87025}}{2 \cdot 1 \cdot 7} =\]

\[= \frac{215 - 295}{34} = \frac{- 80}{34} = - 2\frac{12}{34} =\]

\[= - 2\frac{6}{17}\ (не\ подходит).\]

\[120 \cdot \frac{1}{x} = 120 \cdot \frac{1}{15} = 8\ \left( м^{3} \right) -\]

\[заполнила\ первая\ труба.\]

\[Ответ:8\ м^{3}.\]