От станции C и D, расстояние между которыми равно 270 км, отправились одновременно навстречу друг другу два поезда. Первый поезд прибыл на станцию D через 2 ч 24 мин после встречи, а второй на станцию C – через 3 ч 45 мин после встречи. Найдите, с какой скоростью двигался каждый поезд и через какое время после начала движения состоялась их встреча?

Ответ:

\[Пусть\ x\ \frac{км}{ч} - скорость\ \]

\[с\ горы,\ тогда\ (x - 3)\frac{км}{ч} -\]

\[скорость\ на\ подъеме.\ \]

\[y\ км - длина\ спуска;\ \]

\[(30 - y)\ км - длина\ подъема.\]

\[2\ ч\ 12\ мин = 2\frac{1}{5} = \frac{11}{5}\ ч;\ \ \ \]

\[2\ ч\ 18\ мин = 2\frac{3}{10} = \frac{23}{10}\ ч.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} \frac{y}{x} + \frac{30 - y}{x - 3} = \frac{11}{5}\text{\ \ \ \ \ \ \ \ } \\ \frac{30 - y}{x} + \frac{y}{x - 3} = \frac{23}{10} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} \frac{xy - 3y + 30x - xy}{x(x - 3)} = \frac{11}{5}\text{\ \ \ \ \ \ \ \ \ \ } \\ \frac{30x - 90 - xy + 3y + xy}{x(x - 3)} = \frac{23}{10} \\ \end{matrix} \right.\ \text{\ \ \ \ }\]

\[\left\{ \begin{matrix} \frac{30x - 3y}{x^{2} - 3x} = \frac{11}{5}\text{\ \ \ \ \ \ \ \ \ \ } \\ \frac{30x + 3y - 90}{x^{2} - 3x} = \frac{23}{10} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ }\]

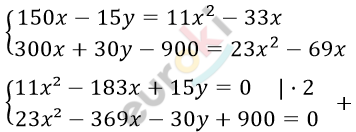
\[45x² - 735x + 900 = 0\ \ \ |\ :5\]

\[9x^{2} - 147x + 180 = 0\]

\[D = 21\ 609 - 6480 =\]

\[= 15129 = 123^{2}\]

\[x = \frac{147 + 123}{18} = 15\ \left( \frac{км}{ч} \right) -\]

\[скорость\ с\ горы.\]

\[x = \frac{147 - 123}{18} =\]

\[= \frac{4}{3}\ (не\ подходит).\]

\[15 - 3 = 12\ \left( \frac{км}{ч} \right) - скорость\ \]

\[вверх.\]

\[Ответ:12\frac{км}{ч};15\frac{км}{ч}\text{.\ }\]