От пристани M на станцию N, расстояние между которыми равно 240 км, отправились одновременно два поезда. Первый поезд прибыл на станцию N на 48 мин позже второго. Найдите скорость каждого поезда, если известно, что первый поезд за 2 ч проходит на 40 км больше, чем второй за 1 ч, и скорость каждого поезда не превышает 100 км/ч.

Ответ:

\[Пусть\ скорость\text{\ I}\ поезда\ \ \]

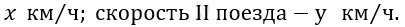
\[2\ ч\ 15\ минут = \frac{215}{60} = 2\frac{1}{4}\ ч =\]

\[= \frac{9}{4}\ ч.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} 5 \cdot (x + y) = 450\ \ \ \ |\ :5 \\ \frac{450}{x} - \frac{450}{y} = \frac{9}{4}\ \ \ \ \ \ \ \ |\ :9 \\ \end{matrix}\text{\ \ \ \ \ } \right.\ \]

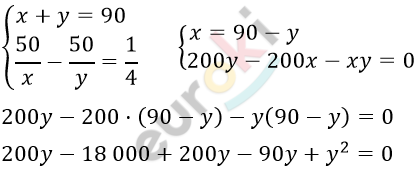
\[y^{2} + 310y - 18\ 000 = 0\]

\[D = 96\ 100 + 72\ 000 =\]

\[= 168\ 100 = 410^{2}\]

\[y = \frac{- 310 - 410}{2} < 0;\ \ \ \ \ \ \ \ \ \]

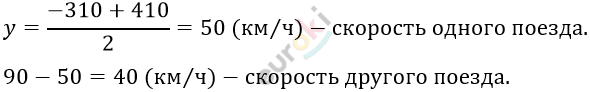
\[Ответ:50\ \frac{км}{ч;\ \ \ 40\ \frac{км}{ч.}}\]