Из пунктов A и B одновременно навстречу друг другу выехали два автомобиля, и после встречи каждый из них продолжил движение в первоначальном направлении. Первый из них, скорость которого на 15 км/ч больше скорости второго, прибыл в пункт A через 3 ч после встречи, а второй в пункт B – через 5 ч 20 мин. Найдите скорость, с которой двигался каждый автомобиль. Через какое время после начала движения состоялась их встреча?

Ответ:

\[5\ ч\ 20\ минут = 5\frac{1}{3}ч = \frac{16}{3}\ ч.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} tx = 3 \cdot (x + 15) \\ t(x + 15) = \frac{16}{3}x \\ \end{matrix}\text{\ \ \ \ \ \ \ } \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} tx = 3x + 45\ \ \ \ \ \\ tx + 15t = \frac{16}{3}x \\ \end{matrix}\text{\ \ \ \ } \right.\ \]

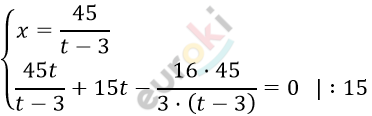
\[\left\{ \begin{matrix} x = \frac{45}{t - 3}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \frac{3t}{t - 3} + t - \frac{16}{t - 3} = 0 \\ \end{matrix} \right.\ \]

\[\frac{3t - 16}{t - 3} + t = 0\]

\[3t - 16 + t² - 3t = 0\]

\[t^{2} = 16\]

\[t = \pm 4.\]

\[4\ часа - время\ встречи.\]

\[Ответ:4\ ч,\ \ \ 45\ \frac{км}{ч,\ \ \ 60\ \frac{км}{ч.}}\]