Не выполняя построения, найдите координаты точек пересечения: прямой x-y-5=0 и окружности (x-3)^2+(y+1)^2=13.

\[\left\{ \begin{matrix} \ x - y - 5 = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ (x - 3)^{2} + (y + 1)^{2} = 13 \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]

\[\left\{ \begin{matrix} y = x - 5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ (x - 3)^{2} + (x - 5 + 1)^{2} = 13 \\ \end{matrix} \right.\ \text{\ \ \ }\]

\[\left\{ \begin{matrix} y = x - 5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ (x - 3)^{2} + (x - 4)^{2} = 13 \\ \end{matrix} \right.\ \]

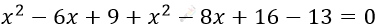
\[2x² - 14x + 12 = 0\ \ |\ :2\]

\[x^{2} - 7x + 6 = 0\]

\[x_{1} + x_{2} = 7,\ \ \ x_{1} \cdot x_{2} = 6\]

\[x_{1} = 6,\ \ x_{2} = 1\]

\[\left\{ \begin{matrix} x = 6 \\ y = 1 \\ \end{matrix} \right.\ \ \ \ или\ \ \left\{ \begin{matrix} x = 1\ \ \ \ \\ y = - 4 \\ \end{matrix} \right.\ \]

\[Ответ:(6;1);\ \ (1;\ - 4).\]