Найдите знаменатель геометрической прогрессии, для которой отношение суммы третьего, четвертого и пятого членов прогрессии к сумме третьего и четвертого членов равно 7/3.

\[\frac{x_{1}q^{2} + x_{1}q^{3} + x_{1}q^{4}}{x_{1}q^{2} + x_{1}q^{3}} =\]

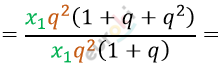
\[= \frac{1 + q + q^{2}}{1 + q}\]

\[\frac{1 + q + q^{2}}{1 + q} = \frac{7}{3}\]

\[3 \cdot \left( 1 + q + q^{2} \right) = 7 \cdot (1 + q)\]

\[3 + 3q + 3q^{2} = 7 + 7q\]

\[3q^{2} + 3q + 3 - 7q - 7 = 0\]

\[3q^{2} - 4q - 4 = 0\]

\[q_{1} = - \frac{2}{3};\ \ q_{2} = 2\]

\[Ответ:\ - \frac{2}{3}\ \ \ или\ \ 2.\]