Найдите значения a, при которых выполняется при всех действительных значениях x неравенство: ax^2-4x+a+3<0.

Ответ:

\[ax^{2} - 4x + a + 3 < 0\]

\[Неравенство\ всегда\ верно\ \]

\[при\ D < 0.\]

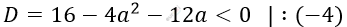
\[a^{2} + 3a - 4 > 0\]

\[a^{2} + 3a - 4 = 0\]

\[a_{1} + a_{2} = - 3;\ \ \ \ \ a_{1} = - 4\]

\[a_{1}a_{2} = - 4;\ \ \ \ \ \ \ \ \ \ \ a_{2} = 1\]

\[(a + 4)(a - 1) > 0\]

\[a < - 4;\ \ \ a > 1.\]

\[Ветви\ параболы\ направлены\ \]

\[вниз:\]

\[a < 0.\]

\[Ответ:( - \infty;\ - 4).\]