Найдите стороны прямоугольника, если их разность равна 14 дм, а диагональ треугольника равна 26 дм.

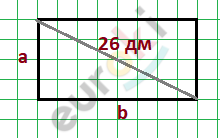
\[Пусть\ a - ширина\ \]

\[прямоугольника,\ а\ b - его\ \]

\[длина.\]

\[По\ условию\ задачи,\ b - a =\]

\[= 14\ дм\ \ и\ диагональ\ равна\ \]

\[26\ дм.\]

\[Составим\ уравнение:\]

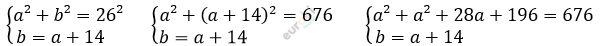
\[2a^{2} + 28a - 480 = 0\ \ \ \ \ |\ :2\]

\[a² + 14a - 240 = 0\ \ \]

\[D = b^{2} - 4ac =\]

\[= 196 - 4 \cdot 1 \cdot ( - 240) =\]

\[= 196 + 960 = 1156\]

\[a_{1} = \frac{- 14 + 34}{2} = \frac{20}{2} = 10\ дм.\]

\[a_{2} = \frac{- 14 - 34}{2} = - \frac{48}{2} =\]

\[= - 24 \Longrightarrow не\ подходит.\]

\[1)\ 10 + 14 = 24\ (дм).\]

\[Ответ:стороны\ \]

\[прямоугольника\ 10\ дм\ \ и\ \]

\[24\ дм.\]