Два поезда отправились одновременно от станции A и B навстречу друг другу, и после встречи каждый продолжил движение в первоначальном направлении. Первый из них, скорость которого на 10 км/ч меньше скорости второго, прибыл на станцию B через 3 ч 36 мин после встречи, а второй на станцию A – через 2 ч 30 мин после встречи. Найдите скорость, с которой двигался каждый поезд. Через какое время после начала движения состоялась их встреча?

Ответ:

\[Пусть\ x\ \frac{км}{ч} - скорость\ \]

\[І\ поезда,\ \]

\[(x + 10)\ \frac{км}{ч} - скорость\]

\[ІІ\ поезда,\ а\ t - время\ встречи.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} t(x + 20) = 3\frac{36}{60}x \\ tx = 2,5 \cdot (x + 10) \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} tx + 10t - 3\frac{3}{5}x = 0 \\ tx = 2,5x + 25\ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]

\[\left\{ \begin{matrix} tx + 10t - \frac{18}{5}x = 0 \\ x(t - 2,5) = 25\ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

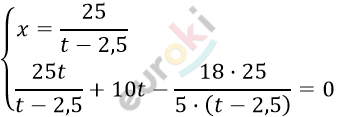
\[125t + 50t² - 450 - 125t = 0\]

\[50t^{2} = 450\]

\[t^{2} = 9\]

\[t = \pm 3\]

\[t = 3\ (ч) - время\ встречи.\ \]

\[x = 50\ \left( \frac{км}{ч} \right) - скорость\ \]

\[первого\ поезда.\]

\[50 + 10 = 60\ \left( \frac{км}{ч} \right) -\]

\[скорость\ второго\ поезда.\]

\[Ответ:50\ \frac{км}{ч};60\ \frac{км}{ч};\]

\[встреча\ через\ 3\ часа.\]