Два экскаватора, работая одновременно, могут вырыть котлован за 6 ч 40 мин. Если же сначала первый экскаватор выроет самостоятельно 4/5 котлована, а затем второй – оставшуюся часть котлована, то вся работа будет выполнена за 12 ч. За сколько часов может вырыть котлован каждый экскаватор, работая отдельно?

\[Пусть\ скорости\ \]

\[велосипедистов\ x\ \frac{км}{ч}\ \]

\[и\ y\ \frac{км}{ч}.\]

\[AC = \frac{1}{3}AB = \frac{1}{3} \cdot 54 = 18\ км;\ \ \ \]

\[BC = 54 - 18 = 36\ км.\]

\[54\ мин = \frac{9}{10}\ ч.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} 2 \cdot (x + y) = 54\ \ \ |\ :2 \\ \frac{36}{y} - \frac{18}{x} = \frac{9}{10}\ \ \ \ \ \ \ |\ :9 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} x + y = 27 \\ \frac{4}{y} - \frac{2}{x} = \frac{1}{10} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} y = 27 - x\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 40x - 20y - xy = 0 \\ \end{matrix} \right.\ \]

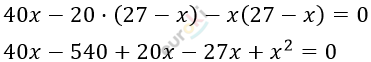
\[x^{2} + 33x - 540 = 0\]

\[D = 1089 + 2160 = 3249 = 57^{2}\]

\[x = \frac{- 33 - 57}{2} < 0\]

\[x = \frac{- 33 + 57}{2} = 12\ \left( \frac{км}{ч} \right) -\]

\[скорость\ одного\ \]

\[велосипедиста.\]

\[27 - 12 = 15\ \left( \frac{км}{ч} \right) -\]

\[скорость\ другого\ \]

\[велосипедиста.\]

\[Ответ:12\ \frac{км}{ч};15\ \frac{км}{ч}.\]