Если одновременно открыть две трубы, через первую из которых в бассейн будет наливаться вода, а через вторую выливаться, то бассейн наполнится за 36 ч. Если 6 ч наполнять бассейн через первую трубу, а затем открыть вторую трубу, через которую вода выливается, то бассейн наполнится через 18 ч после открытия второй трубы. За сколько часов через первую трубку можно наполнить бассейн? За сколько часов через вторую трубу выльется вся вода? Из бассейна?

Ответ:

\[Пусть\ за\ x\ часов\ выроет\ \]

\[первый\ экскаватор,\ \]

\[а\ за\ y\ часов - второй.\]

\[Тогда\ производительности\ \]

\[равны\ \frac{1}{x}\ \ и\ \frac{1}{y}.\]

\[6\ ч\ 40\ мин = 6\frac{40}{60}\ \ ч = 6\frac{2}{3}\ ч =\]

\[= \frac{20}{3}\ ч.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} \frac{20}{3x} + \frac{20}{3y} = 1\ \ \ \ \ \ \ \ \ \ \\ \frac{4x}{5} + \frac{y}{5} = 12\ \ \ \ | \cdot 5 \\ \end{matrix} \right.\ \text{\ \ \ \ }\]

\[\left\{ \begin{matrix} 20y + 20x - 3xy = 0 \\ 4x + y = 60\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ }\]

\[\left\{ \begin{matrix} 20y + 20x - 3xy = 0 \\ y = 60 - 4x\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

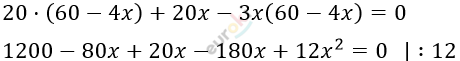
\[x^{2} - 20x + 100 = 0\]

\[(x - 10)^{2} = 0\]

\[x = 10\ (ч) - выроет\ первый\ \]

\[экскаватор.\]

\[60 - 4 \cdot 10 = 20\ (часов) -\]

\[выроет\ второй.\]

\[Ответ:10\ часов;20\ часов.\]