Для каждого значения параметра a решите систему уравнений x-(a+3)y=-1; ax-(3a+9)y=a-6.

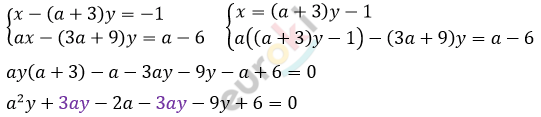
\[\left( a^{2} - 9 \right)y = 2a - 6\]

\[\left( a^{2} - 9 \right)y = 2 \bullet (a - 3)\]

\[a = - 3 \Longrightarrow нет\ решений.\]

\[a = 3 \Longrightarrow решение - \ \]

\[любое\ число\ y \Longrightarrow\]

\[\Longrightarrow (6y - 1;y);y \in R.\]

\[a
eq - 3,\ \ \ a
eq 3:\ \ \ \]

\[\ (a - 3)(a + 3)y = 2 \bullet (a - 3)\]

\[(a + 3)y = 2\]

\[y = \frac{2}{a + 3}\]

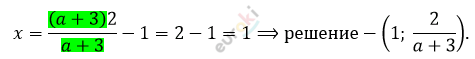
\[Ответ:нет\ решений\ при\ \]

\[a = - 3;(6y - 1;y),\ y \in R\ при\ \]

\[a = 3;\]

\[\left( 1;\ \frac{2}{a + 3} \right)при\ a
eq - 3,\ \ \ a
eq 3.\]