Для каждого значения параметра a решите систему уравнений x-(a+2)y=-1; ax-(2a+4)y=3a-8.

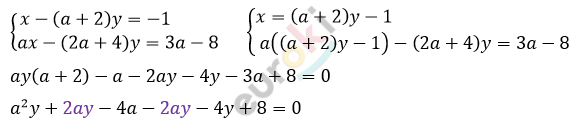
\[y\left( a^{2} - 4 \right) = 4a - 8\]

\[\left( a^{2} - 4 \right)y = 4 \bullet (a - 2)\]

\[1)\ a = - 2 \Longrightarrow нет\ решений.\]

\[2)\ a = 2 \Longrightarrow решение -\]

\[любое\ дейсвительное\ число\ y\]

\[\Longrightarrow (4y - 1;y),\ y \in R.\]

\[3)\ a
eq - 2,\ a
eq 2:\ \ \]

\[(a - 2)(a + 2)y = 4 \bullet (a - 2)\]

\[(a + 2)y = 4\]

\[y = \frac{4}{a + 2}\]

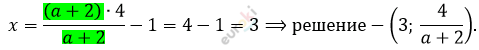
\[Ответ:нет\ решений,\ при\ \]

\[a = - 2;\ \ (4y - 1;y)\ y \in R,\ при\ \]

\[a = 2;\]

\[\text{\ \ \ \ \ \ \ \ \ \ \ \ \ }\left( 3;\ \frac{4}{a + 2} \right)\ при\ a
eq - 2\ \ и\ \]

\[a
eq 2.\]