Вопрос:
13. Путь длиной 28 км первый велосипедист проезжает на 15 минут быстрее второго. Найдите скорость второго велосипедиста, если известно, что она на 2 км/ч меньше скорости первого. Ответ дайте в км/ч. Запишите решение и ответ.
Ответ:
Пусть скорость первого велосипедиста v1, а второго v2. Тогда v2 = v1 - 2. Время первого t1 = 28/v1, время второго t2 = 28/v2. Известно, что t1 = t2 - 15 минут. Переведем минуты в часы: 15 минут = 15/60 = 0.25 часа. Получаем уравнение: 28/v1 = 28/v2 - 0.25. Так как v2 = v1-2, то 28/v1 = 28/(v1-2) - 0.25. Умножим обе части на 4v1(v1-2), чтобы избавиться от дробей: 112(v1-2) = 112v1 - v1(v1-2). 112v1 - 224 = 112v1 - v1² + 2v1. v1² - 2v1 - 224 = 0. Решаем квадратное уравнение: D = 4 - 4 * (-224) = 4 + 896 = 900. Корень из D равен 30. v1 = (2 + 30) / 2 = 16 (второй корень отрицательный не рассматриваем). Скорость второго велосипедиста v2 = v1 - 2 = 16 - 2 = 14. Итоговый ответ: 14 км/ч.
Похожие
- 5. Найдите значение выражения (a - 13) : \frac{a^2 - 26a + 169}{a + 13} при a = 9.
- 6. В среднем 9 керамических горшков из 75 после обжига имеют дефекты. Найдите вероятность того, что случайно выбранный после обжига горшок не имеет дефекта.
- 7. В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 6.
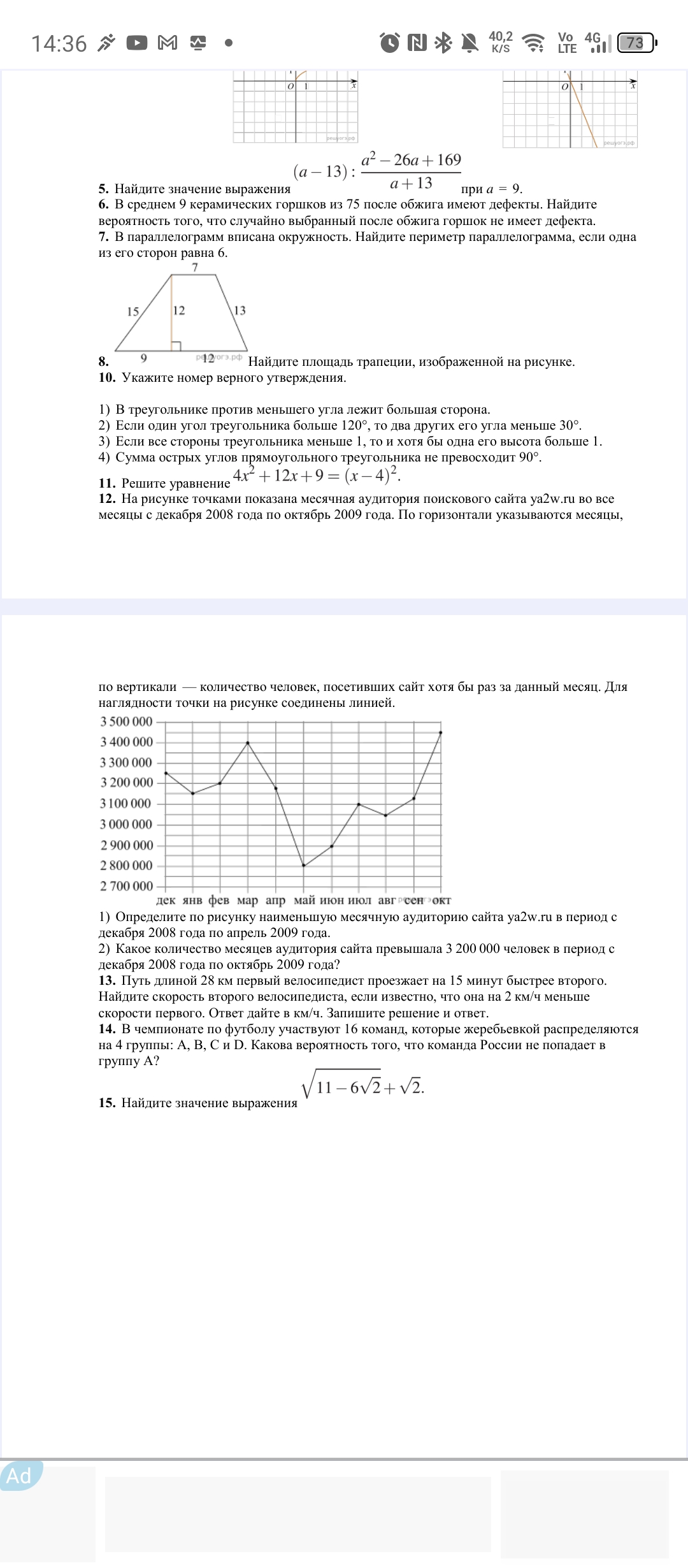
- 8. Найдите площадь трапеции, изображенной на рисунке.
- 10. Укажите номер верного утверждения. 1) В треугольнике против меньшего угла лежит большая сторона. 2) Если один угол треугольника больше 120°, то два других его угла меньше 30°. 3) Если все стороны треугольника меньше 1, то и хотя бы одна его высота больше 1. 4) Сумма острых углов прямоугольного треугольника не превосходит 90°.
- 11. Решите уравнение 4x²+12x+9 = (x-4)².
- 12. На рисунке точками показана месячная аудитория поискового сайта ya2w.ru во все месяцы с декабря 2008 года по октябрь 2009 года. По горизонтали указываются месяцы, по вертикали — количество человек, посетивших сайт хотя бы раз за данный месяц. Для наглядности точки на рисунке соединены линией. 1) Определите по рисунку наименьшую месячную аудиторию сайта ya2w.ru в период с декабря 2008 года по апрель 2009 года. 2) Какое количество месяцев аудитория сайта превышала 3 200 000 человек в период с декабря 2008 года по октябрь 2009 года?
- 13. Путь длиной 28 км первый велосипедист проезжает на 15 минут быстрее второго. Найдите скорость второго велосипедиста, если известно, что она на 2 км/ч меньше скорости первого. Ответ дайте в км/ч. Запишите решение и ответ.
- 14. В чемпионате по футболу участвуют 16 команд, которые жеребьевкой распределяются на 4 группы: А, В, С и D. Какова вероятность того, что команда России не попадает в группу А?
- 15. Найдите значение выражения \sqrt{11-6\sqrt{2}} + \sqrt{2}.