Решебник по математике 6 класс Виленкин контрольные работы Контрольная работа 14 (параграф 43-47). Вариант 2

Условие:

1. На координатной плоскости построй отрезок CD и прямую BE, если С(–3; 6), D(–6;0), В(–6; 5), E(8; –2). Запиши координаты точек пересечения прямой BE с построенным отрезком и осями координат.

2. Построй угол АОК, равный 50°. Отметь на стороне ОА точку М и проведи через нее прямые, перпендикулярные сторонам угла АОК.

3. Построй угол, равный 115°. Отметь внутри этого угла точку N и проведи через нее прямые, параллельные сторонам угла.

4. Начерти на координатной плоскости такую фигуру, абсцисса и ордината любой точки которой удовлетворяют условиям: -1<=x<=4; -2<=y<=2

Решение:

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

\[Точка\ O( - 4;4) \Longrightarrow точка\ \ \]

\[пересечения\ BE\ с\ CD.\]

\[Точки\ \ D( - 6;0);\ \ P(4;0) \Longrightarrow\]

\[точки\ пересечения\ с\ \text{Ox.}\]

\[Точка\ \ M(0;2) \Longrightarrow точка\ \]

\[пересечения\ с\ Oy.\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[\angle AOK = 50{^\circ}\]

\[LM\bot OA;\ \ \ \ MC\bot KO\]

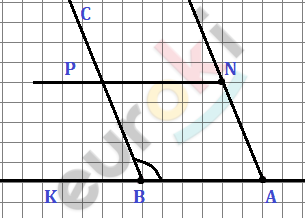
\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[\angle ABC = 115{^\circ}\]

\[NK \parallel BC;\ \ NP \parallel BA.\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

\[- 1 \leq x \leq 4;\ \ \ \ \ - 2 \leq y \leq 2\]