Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 9 класс Атанасян ФГОС Задание 349
Задание 349
\[\boxed{\mathbf{349.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[CM - медиана;\]
\[CH - высота;\]
\[\angle ACH = \angle MCH;\]
\[\angle MCH = \angle MCB.\]
\[\mathbf{Доказать:}\]
\[\mathrm{\Delta}ABC - прямоугольный.\]
\[\mathbf{Доказательство.}\]
\[Пусть\ \angle ACH = \angle MCH =\]
\[= \angle MCB = \alpha.\]
\[1)\ CH - высота\ и\ медиана\]
\[\mathrm{\Delta}ACM:\]
\[\mathrm{\Delta}ACM - равнобедренный \Longrightarrow\]
\[AH = HM = x;\]
\[MB = 2x.\]
\[2)\ Проведем\ MD\bot BC.\]
\[3)\ \mathrm{\Delta}\text{CHM}\ и\ \mathrm{\Delta}CDM -\]
\[прямоугольные:\]
\[CM - общая\ гипотенуза;\ \]
\[\angle MCH = \angle MCB;\]
\[\mathrm{\Delta}MCH = \mathrm{\Delta}MCD\ \]
\[(по\ гипотенузе\ и\ острому\ углу).\]
\[Отсюда:\ \]
\[HM = MD = x.\]
\[4)\ \mathrm{\Delta}MDB - прямоугольный:\]
\[MD = \frac{1}{2}MB \Longrightarrow \angle B = 30{^\circ}.\]
\[5)\ \mathrm{\Delta}BCH - прямоугольный:\]
\[\angle BCH = 90{^\circ} - \angle B =\]
\[= 90{^\circ} - 30{^\circ} = 60{^\circ}.\]
\[6)\ \angle BCH = 2\alpha \Longrightarrow a = \frac{\angle BCH}{2} =\]
\[= \frac{60{^\circ}}{2} = 30{^\circ}.\]
\[Значит:\ \]
\[\angle C = 3 \bullet 30{^\circ} = 90{^\circ};\]
\[\mathrm{\Delta}ABC - прямоугольный.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{349.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
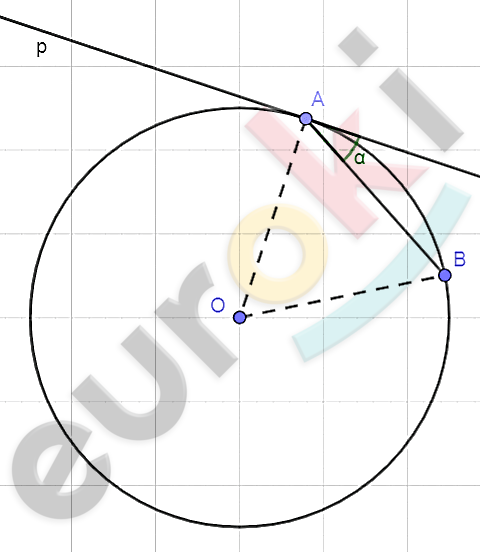
\[p - касательная;\]
\[AB - хорда;\]
\[\text{AB} = r.\]
\[\mathbf{Найти:}\]
\[\angle\alpha - ?\]
\[\mathbf{Решение.}\]
\[1)\ \mathrm{\Delta}\text{AOB} - равносторонний:\]
\[OA = OB\ \]
\[\left( так\ как\ \text{OA\ }и\ OB - радиусы \right);\]
\[AB = r.\]
\[Отсюда:\ \]
\[\angle A = 60{^\circ}.\]
\[2)\ OA\bot p\ \]
\[(по\ свойству\ касательной);\ \]
\[\angle A = 60{^\circ}:\]
\[\ \angle\alpha = 90{^\circ} - 60{^\circ} = 30{^\circ}.\]
\[Ответ:\ \angle\alpha = 30{^\circ}.\]
