Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 773
Задание 773
\[\boxed{\mathbf{773.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Доказать:\]
\[для\ любых\ двух\ векторов\ \overrightarrow{x}\ и\ \overrightarrow{y}\ \ \]
\[справедливо\ неравенство\ \]
\[\left| \overrightarrow{x} - \overrightarrow{y} \right| \leq \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right|;\]
\[в\ каком\ случае\ \]
\[\left| \overrightarrow{x} - \overrightarrow{y} \right| = \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right|?\]
\[Доказательство.\]
\[Разберем\ четыре\ возможных\ \]
\[варианта.\]
\[1)\ Пусть\ \overrightarrow{x}\ и\ \overrightarrow{y}\ неколлинеарные\ \]
\[векторы,\ тогда\ векторы\ \overrightarrow{x}\ и\ \overrightarrow{y},\ а\]
\[также\ \overrightarrow{x} - \overrightarrow{y},\ будут\ сторонами\ \]
\[одного\ треугольника:\]
\[\left| \overrightarrow{x} - \overrightarrow{y} \right| < \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right|\ \]
\[(по\ неравенству\ треугольника).\]
\[2)\ Пусть\ \overrightarrow{x}\ и\ \overrightarrow{y}\ коллинеарны\ и\ \]
\[противоположно\ направлены:\]
\[\left| \overrightarrow{x} - \overrightarrow{y} \right| = \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right|.\]
\[3)\ Пусть\ \overrightarrow{x}\ и\ \overrightarrow{y}\ коллинеарны\ и\ \]
\[сонаправлены:\]
\[\left| \overrightarrow{x} - \overrightarrow{y} \right| < \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right|\ \]
\[\left( так\ как\ \left| \overrightarrow{x} - \overrightarrow{y} \right| = \left| \overrightarrow{x} \right| - \left| \overrightarrow{y} \right| \right).\]
\[4)\ Пусть\ один\ из\ векторов\ \]
\[нулевой:\]
\[\ \left| \overrightarrow{x} - \overrightarrow{y} \right| = \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right|.\]
\[Отсюда:\ \]
\[\left| \overrightarrow{x} - \overrightarrow{y} \right| \leq \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right|.\]
\[Что\ и\ требовалось\ доказать.\]
\[Вопрос:в\ каком\ случае\ \]
\[\left| \overrightarrow{x} - \overrightarrow{y} \right| = \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right|?\]
\[\left| \overrightarrow{x} - \overrightarrow{y} \right| = \left| \overrightarrow{x} \right| + \left| \overrightarrow{y} \right| \Longrightarrow \ когда\ \]
\[векторы\ \overrightarrow{x} \uparrow \downarrow \overrightarrow{y},\ либо\ \overrightarrow{x} = \overrightarrow{0}\ или\ \]
\[\overrightarrow{y} = \overrightarrow{0}\text{.\ }\]
\[\boxed{\mathbf{773.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
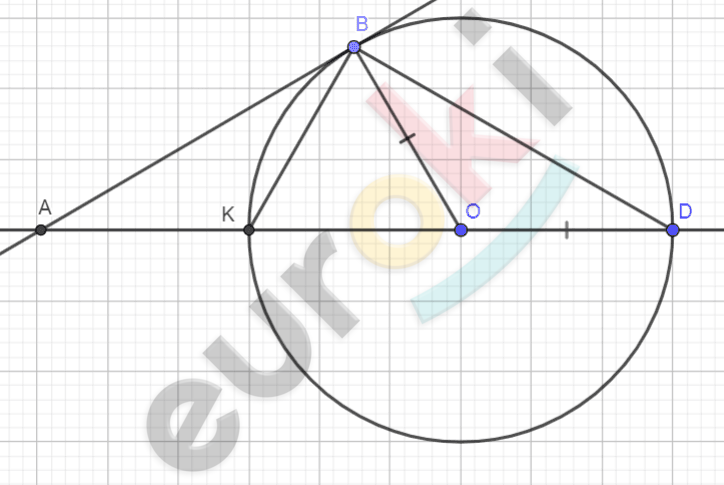
\[\mathbf{Дано:}\]
\[окружность\ (O,\ R);\ \]
\[AB - касател;\]
\[AD - секущая;\]
\[\cup BD = 110{^\circ}20^{'}.\]
\[\mathbf{Найти:}\]
\[\angle BAD - ?\ \]
\[\angle ADB - ?\]
\[\mathbf{Решение.}\]
\[1)\ \angle BKD - вписанный:\]
\[\angle BKD = \frac{1}{2} \cup BD\ \]
\[(по\ теореме\ о\ вписанном\ угле).\]
\[Отсюда:\]
\[\angle BKD = \frac{1}{2} \bullet 110{^\circ}20^{'} = 55{^\circ}10^{'}.\]
\[2)\ O \in AD\ и\ K \in AD \Longrightarrow\]
\[\Longrightarrow \ \cup KD = 180{^\circ}.\]
\[3)\ \angle DBK - вписанный:\ \]
\[\angle DBK = \frac{1}{2} \cup KD\ \]
\[(по\ теореме\ о\ вписанном\ угле).\]
\[Отсюда:\]
\[\angle DBK = \frac{1}{2} \bullet 180{^\circ} = 90{^\circ}.\]
\[4)\ В\ \ \ \mathrm{\Delta}DBK:\]
\[\angle D = 180{^\circ} - \angle BKD - \angle DBK =\]
\[= 90{^\circ} - 55{^\circ}10^{'} = 34{^\circ}50^{'}.\]
\[\angle ADB = \angle D = 34{^\circ}50^{'}.\]
\[5)\ \ \mathrm{\Delta}BOD - равнобедренный:\]
\[BO = OD = R.\]
\[Отсюда:\ \]
\[\angle DBO = \angle BDO = 34{^\circ}50^{'}.\]
\[6)\ \angle DBA = \angle DBO + \angle OBA =\]
\[= 34{^\circ}50^{'} + 90{^\circ} = 124{^\circ}50^{'}.\]
\[7)\ \angle BAD =\]
\[= 180{^\circ} - \left( 124{^\circ}50^{'} + 34{^\circ}50^{'} \right) =\]
\[= 20{^\circ}20^{'}.\]
\[Ответ:\angle BAD = 20{^\circ}20^{'};\ \]
\[\angle ADB = 34{^\circ}50'.\]
