Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 617
Задание 617
\[\boxed{\mathbf{617.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - ромб;\]
\[M,N,P,Q - середины\ сторон.\]
\[\mathbf{Доказать:}\]
\[MNPQ - прямоугольник.\]
\[\mathbf{Доказательство.}\]
\[1)\ Рассмотрим\ \mathrm{\Delta}ABC:\]
\[M - середина\ AB;\ \]
\[N - середина\ BC \Longrightarrow\]
\[\Longrightarrow MN - средняя\ линия \Longrightarrow \ \]
\[\Longrightarrow MN \parallel AC\ и\ MN = \frac{1}{2}\text{AC.}\]
\[2)\ Рассмотрим\ \mathrm{\Delta}ADC:\]
\[P - середина\ DC;\ \]
\[Q - середина\ \text{AD} \Longrightarrow\]
\[PQ - средняя\ линия \Longrightarrow\]
\[\Longrightarrow \ PQ \parallel AC\ и\ QP = \frac{1}{2}\text{AC.}\]
\[3)\ Рассмотрим\ \mathrm{\Delta}ABD:\]
\[M - середина\ AB;\]
\[Q - середина\ \text{AD} \Longrightarrow\]
\[MQ - средняя\ линия \Longrightarrow\]
\[\Longrightarrow MQ \parallel BD\ и\ MQ = \frac{1}{2}\text{BD.}\]
\[4)\ Рассмотрим\ \mathrm{\Delta}BCD:\]
\[N - середина\ BC;\]
\[P - середина\ \text{DC} \Longrightarrow\]
\[NP - средняя\ линия \Longrightarrow\]
\[\Longrightarrow NP \parallel BD\ и\ NP = \frac{1}{2}\text{BD.}\]
\[5)\ MN \parallel AC\ и\ PQ \parallel AC:\]
\[\ MN \parallel PQ\ и\ MN = PQ.\]
\[6)\ MQ \parallel BD\ и\ NP \parallel BD:\]
\[MQ \parallel NP\ и\ MQ = NP.\]
\[7)\ ABCD - ромб:\ \]
\[BD\bot AC\ (по\ свойству);\]
\[MN\bot MQ.\]
\[8)\ MN \parallel PQ\ и\ MQ \parallel NP:\]
\[MNPQ - параллелограмм;\]
\[MN\bot PQ \Longrightarrow\]
\[\Longrightarrow \ MNPQ - прямоугольник.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{617}\mathbf{.}\mathbf{еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - трапеция;\]
\[BC = a;AD = b;\]
\[MN \parallel AD;\]
\[S_{\text{AMND}} = S_{\text{MBCN}}.\]
\[\mathbf{Найти:}\]
\[MN - ?\]
\[\mathbf{Решение.}\]
\[1)\ MN = x.\]
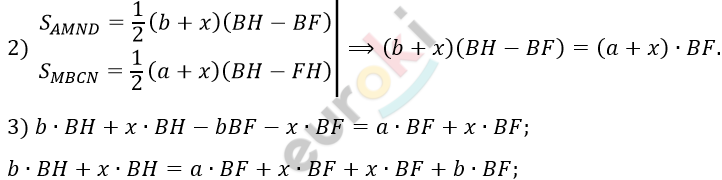
\[(b + x)BH = (a + b + 2x)\text{BF.}\]
\[4)\ S_{\text{ABCD}} = S_{\text{AMND}} + S_{\text{MBCN}}\]
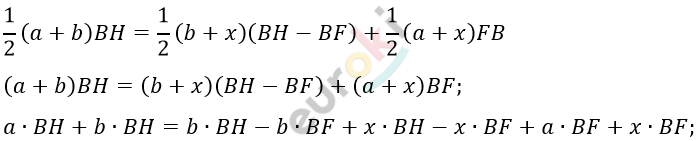
\[aBH - xBH = aBF - bBF;\]
\[(a - x)BH = (a - b)\text{BF.}\]
\[5)\ \left\{ \begin{matrix} (b + x)BH = (a + b + 2x)\text{BF} \\ (a - x)BH = (a - b)\text{BF\ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} BH = \frac{a + b + 2x}{b + x} \bullet BF \\ BH = \frac{a - b}{a - x} \bullet BF\ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[6)\ (a - x)(a + b + 2x) =\]
\[= (b + x)(a - b)\]
\[a^{2} + ab + 2ax - ax - bx - 2x^{2} =\]
\[= ba - b^{2} + ax - bx\]
\[a^{2} + 2ax - ax - 2x^{2} + b^{2} - ax =\]
\[= 0\]
\[a^{2} - 2x^{2} + b^{2} = 0\]
\[2x^{2} = a^{2} + b^{2}\]
\[x^{2} = \frac{a^{2} + b^{2}}{2}\]
\[x = \frac{\sqrt{a^{2} + b^{2}}}{2}.\]
\[Ответ:MN = \frac{\sqrt{a^{2} + b^{2}}}{2}.\]
