Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 1060
Задание 1060
\[\boxed{\mathbf{1060.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[\textbf{а)}\ AB = 8\ см;\ \angle A = 30{^\circ};\ \]
\[\angle B = 45{^\circ}:\]
\[1)\ \angle C = 180{^\circ} - (30{^\circ} + 45{^\circ}) =\]
\[= 180{^\circ} - 75{^\circ} = 105{^\circ}.\]
\[2)\ По\ теореме\ синусов:\]
\[\frac{\text{AB}}{\sin{\angle C}} = \frac{\text{AC}}{\sin{\angle B}} = \frac{\text{BC}}{\sin{\angle A}}\]
\[\frac{8}{\sin{105{^\circ}}} = \frac{\text{AC}}{\sin{45{^\circ}}}\]
\[AC = \frac{8\sin{45{^\circ}}}{\sin{105{^\circ}}} = \frac{8 \bullet \frac{\sqrt{2}}{2}}{0,9659} =\]
\[= 5,8564\ см.\]
\[\frac{8}{\sin{105{^\circ}}} = \frac{\text{BC}}{\sin{30{^\circ}}}\]
\[BC = \frac{8\sin{30{^\circ}}}{\sin{105{^\circ}}} = \frac{8 \bullet \frac{1}{2}}{0,9659} =\]
\[= 4,1411\ см.\]
\[\textbf{б)}\ AB = 5\ см;\ \angle C = 60{^\circ};\ \]
\[\angle B = 45{^\circ}:\]
\[1)\ \angle A = 180{^\circ} - (60{^\circ} + 45{^\circ}) =\]
\[= 180{^\circ} - 105{^\circ} = 75{^\circ}.\]
\[2)\ По\ теореме\ синусов:\]
\[\frac{\text{AB}}{\sin{\angle C}} = \frac{\text{AC}}{\sin{\angle B}} = \frac{\text{BC}}{\sin{\angle A}}\]
\[\frac{5}{\sin{105{^\circ}}} = \frac{\text{AC}}{\sin{45{^\circ}}}\]
\[AC = \frac{5\sin{45{^\circ}}}{\sin{60{^\circ}}} = 4,1\ см.\]
\[\frac{5}{\sin{105{^\circ}}} = \frac{\text{BC}}{\sin{75{^\circ}}}\]
\[BC = \frac{5\sin{75{^\circ}}}{\sin{60{^\circ}}} = 5,58\ см.\]
\[\textbf{в)}\ AB = 3\ см;BC = 3,3\ см;\]
\[\angle A = 48{^\circ}30^{'}:\]
\[1)\ По\ теореме\ синусов:\]
\[\frac{\text{AB}}{\sin{\angle C}} = \frac{\text{AC}}{\sin{\angle B}} = \frac{\text{BC}}{\sin{\angle A}}\]
\[\frac{3}{\sin{\angle C}} = \frac{3,3}{\sin{48{^\circ}30^{'}}}\]
\[\sin{\angle C} = \frac{3\sin{48{^\circ}30^{'}}}{3,3} =\]
\[= \frac{0,749}{1,1} = 0,6809\]
\[\angle C = 42{^\circ}55^{'}.\]
\[\frac{3,3}{\sin{48{^\circ}30^{'}}} = \frac{\text{AC}}{\sin{88{^\circ}35^{'}}}\]
\[AC = \frac{3,3\sin{88{^\circ}35^{'}}}{\sin{48{^\circ}30^{'}}} =\]
\[= \frac{3,3 \bullet 0,9997}{0,749} = 4,4\ см.\]
\[2)\ \angle B =\]
\[= 180{^\circ} - \left( 42{^\circ}55^{'} + 48{^\circ}30^{'} \right) =\]
\[= 88{^\circ}35^{'}.\]
\[\textbf{г)}\ AC = 10,4\ см;BC = 5,2\ см;\]
\[\angle B = 62{^\circ}48^{'}:\]
\[1)\ По\ теореме\ синусов:\]
\[\frac{\text{AB}}{\sin{\angle C}} = \frac{\text{AC}}{\sin{\angle B}} = \frac{\text{BC}}{\sin{\angle A}}\]
\[\frac{10,4}{\sin{62{^\circ}48^{'}}} = \frac{5,2}{\sin{\angle A}}\]
\[\sin{\angle A} = \frac{5,2\sin{62{^\circ}48^{'}}}{10,4} =\]
\[= \frac{5,2 \bullet 0,8894}{10,4} = 0,4447\]
\[\angle A = 26{^\circ}24^{'}.\]
\[\frac{10^{'}4}{\sin{62{^\circ}48^{'}}} = \frac{\text{AB}}{\sin{90{^\circ}48^{'}}}\]
\[AB = \frac{10,4\sin{90{^\circ}48^{'}}}{\sin{62{^\circ}48^{'}}} =\]
\[= \frac{10,4 \bullet 0,9999}{0,8894} = 11,69\ см.\]
\[2)\ \angle C =\]
\[= 180{^\circ} - \left( 62{^\circ}48^{'} + 26{^\circ}24^{'} \right) =\]
\[= 90{^\circ}48^{'}.\]
\[\boxed{\mathbf{1060.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[A( - 2; - 2);\]
\[B( - 3;1);\]
\[C(7;7);D(3;1)\]
\[MN - средняя\ линия.\]
\[\mathbf{Написать:}\]
\[уравнения\ прямых\]
\[\textbf{а)}\ \text{AC\ }и\ BD;\]
\[\textbf{б)}\ MN.\]
\[\mathbf{Решение.}\]
\[\textbf{а)}\ 1)\ A( - 2; - 2):\]
\[ax + by + c = 0;\]
\[a \bullet ( - 2) + b \bullet ( - 2) + c = 0;\]
\[- 2a - 2b + c = 0;\ \]
\[- 2a = 2b - c;\]
\[a = \frac{c - 2b}{2} = \frac{c}{2} - b.\]
\[C(7;7):\]
\[ax + by + c = 0;\]
\(7a + 7b + c = 0;7a = - 7b - c;\)
\[a = \frac{- 7b - c}{7} = - b - \frac{c}{7};\]
\[- b - \frac{c}{7} = \frac{c}{2} - b\]
\[\left\{ \begin{matrix} c = 0 \\ a = - b \\ \end{matrix} \right.\ .\]
\[2)\ Уравнение\ прямой\ AC:\]
\[\left. \ ax - ay + 0 = 0\ \ \ \ \ \ \ \ \right|:a\]
\[x - y = 0.\]
\[3)\ B( - 3;1):\]
\[ax + by + c = 0;\]
\[- 3a + b + c = 0;\]
\[a = \frac{b + c}{3}.\]
\[D(3;1):\]
\[ax + by + c = 0;\]
\[3a + b + c = 0;\]
\[b = - 3a - c;\]
\[a = \frac{- 3a - c + c}{3} = - a\]
\[a = 0 \Longrightarrow b = - c.\]
\[4)\ Уравнение\ прямой\ BD:\]
\[ax + by + c = 0\]
\[- cy + c = 0\ \ \ \ |\ :c\]
\[- y + 1 = 0.\]
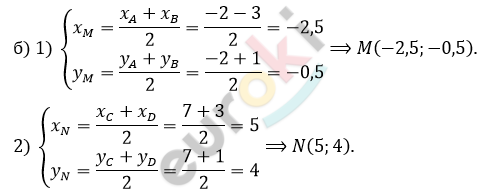
\[3)\ N(5;4):\]
\[5a + 4b + c = 0\]
\[a = \frac{- 4b - c}{5}.\]
\[M( - 2,5; - 0,5):\ \]
\[\left. \ - \frac{5}{2}a - \frac{1}{2}b + c = 0 \right| \bullet 2\]
\[- 5a - b + 2c = 0;b = 2c - 5a\]
\[b = 2c - ( - 4b + c) =\]
\[= 2c + 4b + c + 4b\]
\[- 3b = 3c\]
\[b = - c \Longrightarrow a = \frac{3}{5}\text{c.}\]
\[4)\ Уравнение\ прямой\ MN:\]
\[\left. \ \frac{3}{5}cx - cy + c = 0 \right| \bullet \frac{5}{c}\]
\[3x - 5y + 5 = 0.\]
\[Ответ:\ а)\ x - y =\]
\[= 0\ и\ - y + 1 = 0;\ \]
\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ б)\ 3x - 5y + 5 = 0.\]
