Решебник по геометрии 8 класс Мерзляк Задание 435

\[Схематический\ рисунок.\]

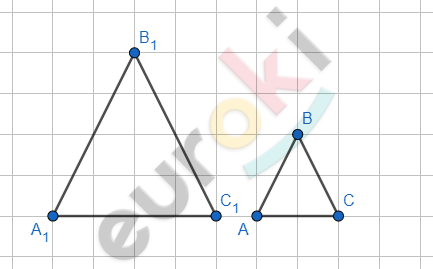
\[Дано:\]

\[\mathrm{\Delta}ABC - равносторонний;\]

\[\mathrm{\Delta}A_{1}B_{1}C_{1} - равносторонний.\]

\[Доказать:\]

\[\mathrm{\Delta}ABC\sim\mathrm{\Delta}A_{1}B_{1}C_{1}.\]

\[Доказательство.\]

\[1)\ \mathrm{\Delta}ABC - \ равносторонний:\]

\[AB = BC = AC;\]

\[\angle A = \angle B = \angle C = 60{^\circ}.\]

\[2)\ \mathrm{\Delta}A_{1}B_{1}C_{1} - равносторонний:\]

\[A_{1}B_{1} = B_{1}C_{1} = A_{1}C_{1};\]

\[\angle A_{1} = \angle B_{1} = \angle C_{1} = 60{^\circ}.\]

\[3)\ \mathrm{\Delta}ABC\sim\mathrm{\Delta}A_{1}B_{1}C_{1}:\]

\[\angle A = \angle A_{1};\ \ \ \]

\[\angle B = \angle B_{1};\ \ \ \]

\[\angle C = \angle C_{1};\]

\[\frac{\text{AB}}{A_{1}B_{1}} = \frac{\text{BC}}{B_{1}C_{1}} = \frac{\text{AC}}{A_{1}C_{1}}.\]

\[Что\ и\ требовалось\ доказать.\]