Решебник по геометрии 7 класс Атанасян ФГОС Задание 985

 

\[\boxed{\mathbf{985.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[точки\ \text{A\ }и\ B;\]

\[BM^{2} - AM^{2} = 2AB^{2}.\]

\[\mathbf{Найти:}\]

\[множество\ точек\ \text{M.}\]

\[\mathbf{Решение.}\]

\[1)\ Введем\ систему\ координат:\]

\[A(0;0);B(a;0);M(x;y).\]

\[2)\ BM^{2} = (a - x)^{2} + y^{2};\]

\[AM^{2} = x^{2} + y^{2};\]

\[AB^{2} = a^{2}.\]

\[3)\ (a - x)^{2} + y^{2} - x^{2} - y^{2} =\]

\[= 2a^{2}\]

\[a^{2} - 2ax + x^{2} + y^{2} - x^{2} - y^{2} =\]

\[= 2a^{2}\]

\[- 2ax = a^{2}\ \]

\[- 2x = a\]

\[x = - \frac{a}{2}.\]

\[4)\ Множество\ всех\ точек\ M:\]

\[прямая,\ перпендикулярная\ \text{AB\ }\]

\[и\ проходящая\ через\ точку,\ \]

\[симметричную\ середине\ \text{AB.}\]

\[\boxed{\mathbf{985}\mathbf{.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\mathbf{\ задачи:}\]

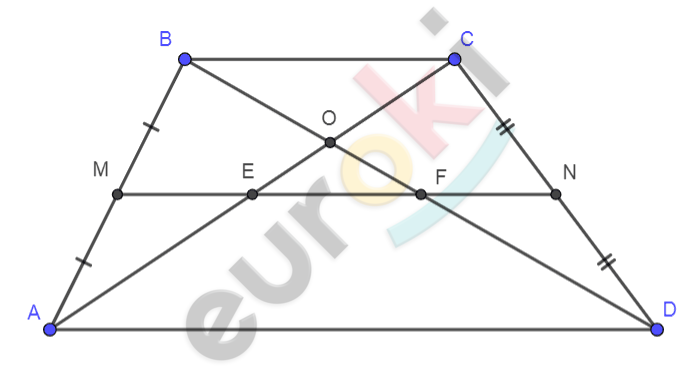
\[\mathbf{Дано:}\]

\[ABCD - трапеция;\]

\[MN - средняя\ линия;\]

\[BD\ и\ AC - диагонали.\]

\[\mathbf{Доказать:}\]

\[MN\ проходит\ через\ E\ и\ F;\]

\[так\ что\]

\[BF = FD;\]

\[AE = EC.\]

\[\mathbf{Доказательство.}\]

\[1)\ MN - средняя\ линия:\]

\[BC \parallel MN \parallel AD.\]

\[2)\ AM = MB;\ \ BC \parallel MN \parallel AD:,\]

\[BF = FD\ (по\ теореме\ Фалеса);\ \]

\[\text{MN\ }проходит\ через\ точку\ F.\]

\[3)\ CN = ND;\ \ BC \parallel MN \parallel AD:\]

\[CE = EA\ (по\ теореме\ Фалеса);\]

\[\text{MN\ }проходит\ через\ точку\ E.\]

\[4)\ Из\ пунктов\ 2\ и\ 3\ делаем\ \]

\[вывод:\]

\[MN\ проходит\ через\ точки\ \]

\[\text{E\ }и\ \text{F.}\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]