Решебник по геометрии 7 класс Атанасян ФГОС Задание 920

 

\[\boxed{\mathbf{920.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[\textbf{а)}\ \overrightarrow{x}\ \left\{ - 3;\frac{1}{5} \right\}\ :\ \]

\[\overrightarrow{x} = - 3\overrightarrow{i} + \frac{1}{5}\overrightarrow{j}\text{\ .}\]

\[\textbf{б)}\ \overrightarrow{y}\ \left\{ - 2;\ - 3 \right\}\ :\ \]

\[\overrightarrow{y} = - 2\overrightarrow{i} - 3\overrightarrow{j}.\]

\[\textbf{в)}\ \overrightarrow{z}\ \left\{ - 1;0 \right\}\ :\ \]

\[\overrightarrow{z} = - \overrightarrow{i}.\]

\[\textbf{г)}\ \overrightarrow{u}\ \left\{ 0;3 \right\}\ :\ \]

\[\overrightarrow{u} = 3\overrightarrow{j}.\]

\[\textbf{д)}\ \overrightarrow{v}\ \left\{ 0;1 \right\}\ :\ \]

\[\overrightarrow{v} = \overrightarrow{j}.\]

\[\boxed{\mathbf{920.еуроки - ответы\ на\ пятёрку}}\]

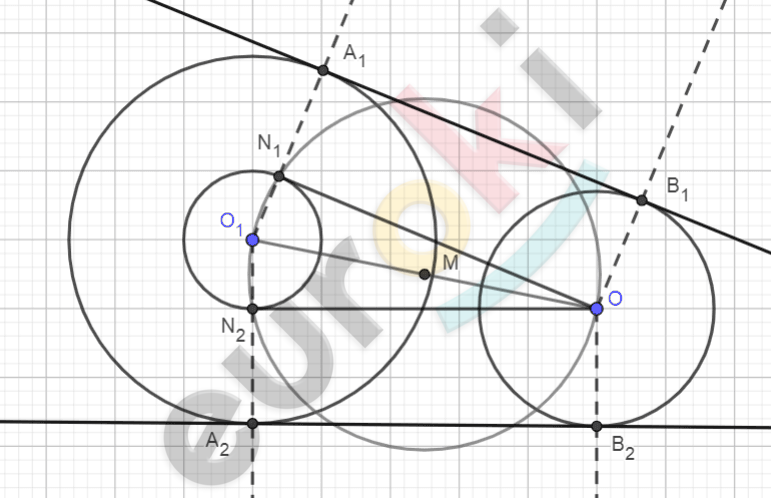
\[Построение.\]

\[1)\ Построим\ окружность\ \]

\[\left( O_{1};R - r \right).\]

\[2)\ Обозначим\ середину\ \]

\[отрезка\ O_{1}\text{O\ }точкой\ M,\ \]

\[построим\ окружность\ (M;O).\]

\[3)\ На\ пересечении\ \]

\[окружностей\ (M;O)\ и\ \]

\[\left( O_{1};R - r \right) - отметим\ точки\]

\[N_{1}\ и\ N_{2}.\]

\[4)\ Построим\ перпендикуляры\ \]

\[к\ отрезкам\ N_{1}\text{O\ }и\ N_{2}\text{O\ }из\ точек\]

\[O_{1}\ и\ O,\ отметим\ точки\ \]

\[A_{1},A_{2},B_{1}\ и\ B_{2}\ на\ пересечении\ \]

\[перпендикуляров\ с\ данными\ \]

\[окружностями.\]

\[5)\ Построим\ прямые\ \]

\[A_{1}B_{1}\ и\ A_{2}B_{2} - искомые\ \]

\[касательные.\]