Решебник по геометрии 7 класс Атанасян ФГОС Задание 917

 

\[\boxed{\mathbf{917.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[\mathbf{Построить:\ }\]

\[\overrightarrow{a}\ \left\{ 3;0 \right\};\ \overrightarrow{b}\ \left\{ 2;\ - 1 \right\};\ \overrightarrow{c}\ \left\{ 0;\ - 3 \right\};\ \]

\[\overrightarrow{d}\ \left\{ 1;1 \right\};\ \overrightarrow{e}\ \left\{ 2;\ \sqrt{2} \right\}\mathbf{.}\]

\[\boxed{\mathbf{917.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\ \]

\[\mathrm{\Delta}ABC;\ \]

\[окружность\ (M;r);\]

\[окружность\ (O;R);\]

\[d = OM.\]

\[Доказать:\]

\[d^{2} = R^{2} - 2Rr.\]

\[Доказательство.\]

\[1)\ Проведем\ через\ точку\ \text{M\ }\]

\[диаметр\ описанной\ \]

\[окружности\ PQ,а\ также\ \]

\[биссектрисы\ AM\ и\ \text{BM}.\]

\[2)\ По\ теореме\ о\ произведении\ \]

\[отрезков\ пересекающихся\ \]

\[хорд:\]

\[PM \bullet MQ = AM \bullet MA_{1};\]

\[(R + d)(R - d) = AM \bullet MA_{1}.\]

\[3)\ AA_{1}\ и\ BB_{1} - биссектрисы:\]

\[\cup BA_{1} = \cup A_{1}C;\]

\[\cup CB_{1} = \cup B_{1}\text{A.}\]

\[Значит:\ \ \]

\[\angle\text{BM}A_{1} = \frac{\cup BA_{1} + \cup AB_{1}}{2} =\]

\[= \frac{\cup A_{1}C + CB_{1}}{2} = \angle MBA_{1}.\]

\[4)\ \mathrm{\Delta}MA_{1}B - равнобедренный;\]

\[(R + d)(R - d) = AM \bullet BA_{1}.\]

\[5)\ Проведем\ диаметр\ A_{1}A_{2}\ \]

\[описанной\ окружности:\]

\[K - точка\ касания\ вписанной\ \]

\[окружности\ и\ стороны\ \text{AB.}\]

\[6)\ \mathrm{\Delta}A_{1}A_{2}B - прямоугольный\ \]

\[(так\ как\ опирается\ на\ диаметр);\]

\[\mathrm{\Delta}AMK - прямоугольный:\]

\[\angle A_{1}A_{2}B = \angle MAK = \frac{1}{2} \cup BA_{1} \Longrightarrow \ \]

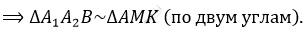
\[Отсюда:\ \]

\[MK\ :BA_{1} = AM\ :A_{1}A_{2}\ \]

\[или\ \]

\[r\ :BA_{1} = AM\ :2R.\]

\[7)\ AM \bullet BA_{1} = 2Rr\]

\[(R + d)(R - d) = 2Rr\]

\[d^{2} = R^{2} - 2Rr.\]

\[Что\ и\ требовалось\ доказать.\]