Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 914
Задание 914
\[\boxed{\mathbf{914.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[\mathbf{Дано:}\ \overrightarrow{a}\ и\ \overrightarrow{b} - неколлинеарны\]
\[\textbf{а)}\ Доказать:\ \]
\[\overrightarrow{a} + \overrightarrow{b}\ и\ \overrightarrow{a} - \overrightarrow{b} - неколлинеарны.\]
\[Доказательство\ от\ противного:\]
\[Пусть\ \overrightarrow{a} + \overrightarrow{b}\ и\ \]
\[\overrightarrow{a} - \overrightarrow{b} - коллинеарны,\ тогда\ по\ \]
\[лемме\ о\ коллинеарных\]
\[векторах:\ \]
\[\overrightarrow{a} + \overrightarrow{b} = k\left( \overrightarrow{a} - \overrightarrow{b} \right)\]
\[\overrightarrow{a} + \overrightarrow{b} = k\overrightarrow{a} - k\overrightarrow{b}\]
\[- \overrightarrow{a} - k\overrightarrow{a} = - \overrightarrow{b} - k\overrightarrow{b}\]
\[\overrightarrow{a}(1 - k) = \overrightarrow{b}( - 1 - k)\]
\[\overrightarrow{a} = \frac{- 1 - k}{1 - k} \bullet \overrightarrow{b}.\]
\[Но\ такое\ разложение\ \]
\[невозможно,\ так\ как\ \overrightarrow{a}\ и\ \overrightarrow{b}\ по\ \]
\[условию\ неколлинеарны.\]
\[Следовательно:\]
\[\overrightarrow{a} + \overrightarrow{b}\ и\ \]
\[\overrightarrow{a} - \overrightarrow{b} - неколлинеарны.\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{б)}\ Доказать:\ \]
\[2\overrightarrow{a} - \overrightarrow{b}\ и\ \]
\[\overrightarrow{a} + \overrightarrow{b} - неколлинеарны.\]
\[Доказательство\ от\ противного:\]
\[Пусть\ 2\overrightarrow{a} - \overrightarrow{b}\ и\ \]
\[\overrightarrow{a} + \overrightarrow{b} - коллинеарны,\ тогда\ по\ \]
\[лемме\ о\ коллинеарных\]
\[векторах:\ \]
\[2\overrightarrow{a} - \overrightarrow{b} = k\left( \overrightarrow{a} + \overrightarrow{b} \right)\]
\[2\overrightarrow{a} - \overrightarrow{b} = k\overrightarrow{a} + k\overrightarrow{b}\]
\[2\overrightarrow{a} - k\overrightarrow{a} = \overrightarrow{b} + k\overrightarrow{b}\]
\[\overrightarrow{a}(2 - k) = \overrightarrow{b}(1 + k)\]
\[\overrightarrow{a} = \frac{1 + k}{2 - k} \bullet \overrightarrow{b}.\]
\[Но\ такое\ разложение\ \]
\[невозможно,\ так\ как\ \overrightarrow{a}\ и\ \overrightarrow{b}\ по\ \]
\[условию\ неколлинеарны.\]
\[Следовательно:\]
\[2\overrightarrow{a} - \overrightarrow{b}\ и\ \]
\[\overrightarrow{a} + \overrightarrow{b} - неколлинеарны.\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{в)}\ Доказать:\ \]
\[\overrightarrow{a} + \overrightarrow{b}\ и\ \]
\[\overrightarrow{a} + 3\overrightarrow{b} - неколлинеарны.\]
\[Доказательство\ от\ противного:\]
\[Пусть\ \overrightarrow{a} + \overrightarrow{b}\ и\ \]
\[\overrightarrow{a} + 3\overrightarrow{b} - коллинеарны,\ тогда\ \]
\[по\ лемме\ о\ коллинеарных\]
\[векторах:\ \]
\[\overrightarrow{a} + \overrightarrow{b} = k\left( \overrightarrow{a} + 3\overrightarrow{b} \right)\]
\[\overrightarrow{a} + \overrightarrow{b} = k\overrightarrow{a} + k3\overrightarrow{b}\]
\[\overrightarrow{a} - k\overrightarrow{a} = k3\overrightarrow{b} - \overrightarrow{b}\]
\[\overrightarrow{a}(1 - k) = \overrightarrow{b}(3k - 1)\]
\[\overrightarrow{a} = \frac{3k - 1}{1 - k} \bullet \overrightarrow{b}.\]
\[Но\ такое\ разложение\ \]
\[невозможно,\ так\ как\ \overrightarrow{a}\ и\ \overrightarrow{b}\ по\ \]
\[условию\ неколлинеарны.\]
\[Следовательно:\]
\[\overrightarrow{a} + \overrightarrow{b}\ и\]
\[\overrightarrow{a} + 3\overrightarrow{b} - неколлинеарны.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{914.еуроки - ответы\ на\ пятёрку}}\]
\[Дано:\]
\[ABCD - вписанный\ \]
\[четырехугольник;\]
\[AC\bot BD.\]
\[Доказать:\]
\[AB^{2} + CD^{2} = d^{2}.\]
\[Доказательство.\]
\[1)\ Проведем\ через\ точку\ M\ \]
\[пересечения\ биссектрис\ \]
\[прямую,\ параллельную\ AB,\ \]
\[отметим\ точки\ \text{E\ }и\ \text{F\ }\]
\[на\ пересечении\ данной\]
\[прямой\ и\ прямых\ \text{AD\ }и\ \text{BC.}\]
\[2)\ Рассмотрим\ \mathrm{\Delta}\text{DEM\ }и\ \mathrm{\Delta}CFM:\]
\[EF \parallel AB;\]
\[\angle A + \angle E =\]
\[= 180{^\circ}\ (как\ односторонние).\]
\[Отсюда:\]
\[\angle E = \angle C;\]
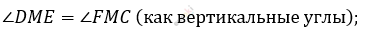
\[\mathrm{\Delta}DEM\sim\ \mathrm{\Delta}\text{CFM.}\]
\[3)\ Точка\ M - точка\ \]
\[пересечения\ биссектрис:\]
\[она\ равноудалена\ от\ прямых\ \]
\[\text{AB\ }и\ AD,\ а\ также\ от\ прямых\ \ \]
\[\text{AB\ }и\ \text{BC.}\]
\[Следовательно,\ она\ \]
\[равноудалена\ от\ прямых\ \]
\[\text{AD\ }и\ \text{BC.}\]
\[Отсюда:\ \]
\[высоты\ \mathrm{\Delta}\text{DEM\ }и\ \mathrm{\Delta}CFM;\]
\[проведенные\ из\ вершины\ M\ \]
\[равны.\]
\[Значит:\ \]
\[\mathrm{\Delta}DEM = \mathrm{\Delta}CFM;\]
\[CF = ED.\]
\[в\ \mathrm{\Delta}AEM:\ \ \]
\[\angle A = \angle M;\]
\[AE = EM.\]
\[Аналогично:\ BF = FM.\]
\[5)\ Таким\ образом:\ \]
\[CD = DM + MC = FM + EM =\]
\[= BF + AE = BC + AD.\]
\[Что\ и\ требовалось\ доказать.\]
