Решебник по геометрии 7 класс Атанасян ФГОС Задание 899

 

\[\boxed{\mathbf{899.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Дано:\]

\[Построить:\]

\[наименьшую\ хорду,\ \]

\[проходящую\ через\ точку\ \text{M.}\]

\[Построение.\]

\[1)\ Проведем\ диаметр\ \text{OM.}\]

\[2)\ Через\ точку\ \text{M\ }построим\ \]

\[перпендикуляр\ к\ \text{OM.}\]

\[3)\ На\ пересечениях\ данного\ \]

\[перпендикуляра\ и\ окружности\]

\[отметим\ точки\ \text{A\ }и\ \text{B.}\]

\[4)\ Хорда\ AB - искомая.\]

\[\boxed{\mathbf{899.еуроки - ответы\ на\ пятёрку}}\]

\[Доказательство.\]

\[Пусть\ окружность\ касается\ \]

\[стороны\ \text{BC\ }и\ продолжения\ \]

\[сторон\ \text{AC\ }и\ \text{AB}\]

\[треугольника\ ABC\ в\ точках\ \]

\[A_{1};B^{'};C^{'}.\]

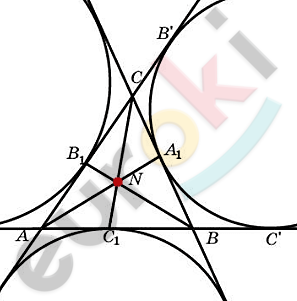
\[Тогда:\]

\[CA_{1} = CB^{'};\]

\[BA_{1} = BA^{'};\]

\[AB^{'} = AC^{'}.\]

\[Пусть\ AB = c;AC = b;BC = a;\]

\[p - полупериметр\ ⊿ABC.\]

\[Получаем:\]

\[AB^{'} = AC^{'} = p;\]

\[BA_{1} = BC^{'} = p - c;\]

\[A_{1}C = CB^{'} = p - b.\]

\[Аналогично\ для\ точек\ \]

\[касания\ B_{1}\ и\ C_{1}:\]

\[AC_{1} = p - b;\]

\[C_{1}B = p - a;\]

\[CB_{1} = p - a;\]

\[C_{1}A = p - b.\]

\[Следовательно,\ выполняется\ \]

\[равенство:\]

\[\frac{A_{1}C}{C_{1}B} \cdot \frac{BA_{1}}{A_{1}C} \cdot \frac{CB_{1}}{B_{1}A} = 1.\]

\[По\ теореме\ Чевы,\ прямые\ AA_{1};\]

\[BB_{1};\ \ CC_{1}\ пересекаются\ \]

\[в\ одной\ точке.\]

\[Что\ и\ требовалось\ доказать.\]