Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 895
Задание 895
\[\boxed{\mathbf{895.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[Дано:\ \]
\[\mathrm{\Delta}ABC;\]
\[O - центр\ описанной\ \]
\[окружности\ (O;R);\]
\[H - точка\ пересечения\ высот\ \]
\[AA_{1},BB_{1},CC_{1};\]
\[A_{2},B_{2},C_{2} - середины\ AH,BH,\]
\[CH;\]
\[A_{3},B_{3},C_{3} - середины\ сторон\ \]
\[\mathrm{\Delta}\text{ABC.}\]
\[Доказать:\]
\[A_{1},A_{2},A_{3},B_{1},B_{2},B_{3},C_{1},C_{2},C_{3} -\]
\[лежат\ на\ одной\ окружности.\]
\[Доказательство.\]
\[1)\ Пусть\ точка\ M - середина\ \]
\[отрезка\ OH;\ \ \ MN\bot AC.\]
\[2)\ HB_{1} \parallel MN \parallel OB_{3} \Longrightarrow\]
\[\Longrightarrow \ B_{1}N = NB_{3}\ \]
\[(по\ теореме\ Фалеса):\]
\[\mathrm{\Delta}B_{1}MN = \mathrm{\Delta}B_{3}\text{MN\ }\]
\[(по\ двум\ катетам).\]
\[Отсюда:\ \]
\[MB_{1} = MB_{3}.\]
\[3)\ Пусть\ B_{4} - точка,\ \]
\[симметричная\ \text{H\ }\]
\[относительно\ \text{AC.}\]
\[Рассмотрим\ \mathrm{\Delta}OHB_{4}:\ \]
\[MB_{1} - средняя\ линия \Longrightarrow\]
\[\Longrightarrow MB_{1} = \frac{OB_{4}}{2},\ но\ точка\ B_{4}\ \]
\[лежит\ на\ окружности,\ \]
\[описанной\ около\ \mathrm{\Delta}\text{ABC\ }\]
\[(задача\ 886):\]
\[MB_{1} = MB_{3} = \frac{R}{2}.\]
\[4)\ MB_{2} - средняя\ линия\ \]
\[\mathrm{\Delta}BOH \Longrightarrow \ MB_{2} = \frac{\text{OB}}{2} = \frac{R}{2};\]
\[MB_{1} = MB_{2} = MB_{3} = \frac{R}{2};\]
\[5)\ Аналогично:\ \]
\[для\ MA_{1} = MA_{2} = MA_{3} = \frac{R}{2}\ и\ \]
\[MC_{1} = MC_{2} = MC_{3} = \frac{R}{2}.\]
\[6)\ Следовательно:\ \]
\[A_{1},A_{2},A_{3},B_{1},B_{2},B_{3},C_{1},C_{2},C_{3} -\]
\[лежат\ на\ одной\ окружности\ \]
\[\left( M;\frac{R}{2} \right).\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{895.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
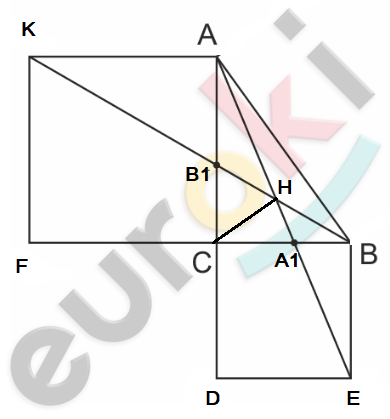
\[Доказательство.\]
\[Пусть\ BC = a;\ \ AC = b.\]
\[Введем\ систему\ координат\ \]
\[с\ началом\ в\ точке\ C\ (0;0);\]
\[координаты\ других\ точек:\]
\[A(0;b);B(a;0);K( - b;b);\ \]
\[\text{\ E}(a; - a).\]
\[CB_{1} = CA_{1} = \frac{\text{ab}}{a + b};то:\]
\[A_{1}\left( \frac{\text{ab}}{a + b};0 \right);\ \ B_{1}\left( 0;\frac{\text{ab}}{a + b} \right).\]
\[Запишем\ уравнение\ прямых\ \]
\[\text{BK\ }и\ \text{AE.}\]
\[Прямая\ BK\ проходит\ через\ \]
\[точки\ B(a;0);K( - b;b):\]
\[y = - \frac{b}{a + b}x + \frac{\text{ab}}{a + b}.\]
\[Прямая\ AE\ проходит\ через\ \]
\[точки\ A(0;b);\ \ E(a; - a):\]
\[y = - \frac{b(a + b)}{\text{ab}}x + b =\]
\[= - \frac{a + b}{a}x + b.\]
\[H - точка\ пересечения\ \]
\[данных\ прямых;найдем\ ее\ \]
\[кординаты:\]
\[\left\{ \begin{matrix} - \frac{b}{a + b}x + \frac{\text{ab}}{a + b} = - \frac{a + b}{a}x + b \\ y = - \frac{\text{bx}}{a + b} + \frac{\text{ab}}{a + b}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]
\[Отсюда:\]
\[x = \frac{ab^{2}}{a^{2} + ab + b^{2}};\ \ \ \]
\[y = \frac{a²b}{a^{2} + ab + b^{2}}.\]
\[Найдем\ скалярное\ \]
\[произведение\ векторов:\]
\[\overrightarrow{\text{AB}}(a; - b);\ \ \]
\[\overrightarrow{\text{CH}}\left( \frac{ab^{2}}{a^{2} + ab + b^{2}};\ \frac{a^{2}b}{a^{2} + ab + b^{2}} \right).\]
\[\overrightarrow{\text{AB}}\bot\overrightarrow{\text{CH}}:\]
\[точка\ \text{H\ }лежит\ на\ высоте\ \text{CH\ }\]
\[треугольника\ ABC.\]
\[Что\ и\ требовалось\ доказать.\ \]
