Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 873
Задание 873
\[\boxed{\mathbf{873.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Дано:\ \]
\[углы\ \text{α\ }и\ \gamma;\ \]
\[отрезок\ \text{a.}\]
\[Построить:\]
\[\mathrm{\Delta}ABC;\ \]
\[\angle A = \alpha;\]
\[\angle C = \gamma;\]
\[AC + BH = a;\]
\[BH - высота.\]
\[\mathbf{Построение.}\]
\[1)\ Проводим\ прямую\ f,\ \]
\[выбираем\ на\ ней\ точку\ A,\ \]
\[откладываем\ \]
\[произвольный\ отрезок\ AC_{1}.\]
\[2)\ Строим\ \angle A = \alpha\ и\ \angle C_{1} = \gamma.\ \]
\[Отмечаем\ точку\ пересечения\ \]
\[B_{1}.\]
\[3)\ Опускаем\ перпендикуляр\ \]
\[B_{1}\text{H\ }на\ AC_{1}\text{.\ \ }\]
\[Отмечаем\ H = B_{1}H \cap AC_{1}.\]
\[Подобный\ треугольник\ AB_{1}C_{1}\ \]
\[построен.\]
\[4)\ Проводим\ от\ точки\ A\ луч\ \text{AR}\ \]
\[под\ произвольным\ острым\ \]
\[углом\ к\ AC.\]
\[Отмечаем\ точки\ R_{1}и\ R:\ \]
\[AR_{1} = \ AC_{1} + B_{1}H_{1};\ \ AR = a.\]
\[5)\ Проведем\ прямую\ R_{1}C_{1}\ и\ \]
\[параллельную\ ей\ \text{RC}\ \parallel R_{1}C_{1}.\ \]
\[Отмечаем\ точку\ пересечения\ \]
\[C = \ \text{RC}\ \cap \ AC_{1}.\]
\[6)\ Проводим\ прямую\ CB \parallel C_{1}B_{1}.\ \]
\[Отмечаем\ точку\ пересечения\]
\[B = CB \cap AB_{1}\text{.\ }\]
\[Масштабирование\ завершено.\ \]
\[Треугольник\ ABC\ - \ искомый.\]
\[Задача\ имеет\ решение\ для\ \]
\[любого\ отрезка\ a\ при\ условии:\ \]
\[\alpha + \gamma\ < \ 180{^\circ}.\]
\[\boxed{\mathbf{873.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
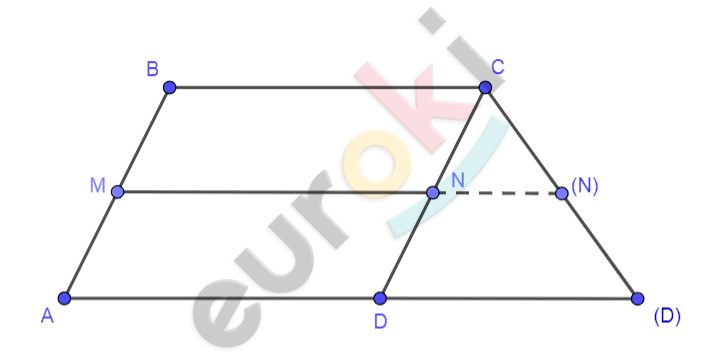
\[ABCD - выпуклый\ \ \]
\[четырехугольник;\]
\[M \in AB;N \in CD;\]
\[AM = MB;\]
\[CN = ND;\]
\[MN = \frac{AB + BC}{2}.\]
\[\mathbf{Доказать:}\]
\[\text{ABCD} - параллелограмм\ или\ \]
\[трапеция.\]
\[\mathbf{Доказательство.}\]
\[1)\ Если\ стороны\ \]
\[четырехугольника\ попарно\ \]
\[не\ параллельны:\]
\[MN < \frac{AB + BC}{2}.\]
\[2)\ Пусть\ AD \nparallel BC;\ \ AB \parallel CD:\]
\[MN \leq \frac{AD + BC}{2}\text{.\ }\]
\[Неравенство\ \ характерно\ для\ \]
\[равнобедренной\ трапеции.\]
\[3)\ Пусть\ \text{AD} \parallel \text{BC};\ \ \Longrightarrow \text{MN} =\]
\[= \frac{\text{AB} + \text{BC}}{2}:\]
\[в\ любом\ случае,\ независимо\ \]
\[от\ того,\ как\ расположены\ \]
\[пары\ других\ сторон.\ \]
\[Следовательно:\]
\[\text{ABCD} - параллелограмм\ или\ \]
\[трапеция.\]
\[Что\ и\ требовалось\ доказать.\ \ \]
