Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 861
Задание 861
\[\boxed{\mathbf{861.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - трапеция;\]
\[AB \parallel CD;\]
\[AB < CD;\]
\[O = AC \cap BD;\]
\[\mathrm{\Delta}AOB - равносторонний;\]
\[M \in OA;\ \]
\[N \in BC;\]
\[K \in OD;\]
\[AM = MO;\]
\[BN = NC;\]
\[OK = KD.\]
\[\mathbf{Доказать:}\]
\[\mathrm{\Delta}MNK - равносторонний.\]
\[\mathbf{Доказательство.}\]
\[1)\ Пусть\ OA = OB = AB = a;\ \ \]
\[CD = b.\]
\[2)\ Проведем\ прямую\ KE \parallel CD;\ \]
\[E \in OC;\ KE \parallel CD \parallel AB:\ \]
\[\angle AOB = \angle KOE\ \]
\[(как\ вертикальные);\]
\[следовательно:\]
\[\mathrm{\Delta}KOE\sim\mathrm{\Delta}BOA\ (по\ двум\ углам);\]
\[\mathrm{\Delta}KOE - равносторонний.\]
\[3)\ KE - средняя\ линия\ \mathrm{\Delta}DOC:\]
\[KE = \frac{1}{2}CD = \frac{b}{2} = OK = OE.\]
\[4)\ Аналогично - \ \mathrm{\Delta}DOC\sim\mathrm{\Delta}BOA:\ \]
\[\mathrm{\Delta}DOC - равносторонний;\ \]
\[OC = OD = CD = b\]
\[Значит:\]
\[5)\ NE - средняя\ линия\ \mathrm{\Delta}COB:\]
\[NE = \frac{1}{2}OB = \frac{a}{2};\ \]
\[NE \parallel OB;\ \]
\[значит:\]
\[\angle NEO = \angle BOA = 60{^\circ}.\]
\[6)\ KO = KE = \frac{b}{2};\ \ \]
\[OM = EN = \frac{a}{2};\]
\[\angle KOM = \angle KEN = 120{^\circ};\ \]
\[следовательно:\]
\[\mathrm{\Delta}KOM = \mathrm{\Delta}KEN;\ \ \]
\[KM = KN;\ \]
\[\angle MKO = \angle NKE.\]
\[7)\ \angle MKN =\]
\[= \angle OKE + \angle MKO - \angle NKE =\]
\[= 60{^\circ}.\]
\[8)\ \mathrm{\Delta}MNK - равнобедренный:\]
\[KM = KN;\ \]
\[с\ углом\ по\ вершине\ \]
\[\angle MKN = 60{^\circ}.\]
\[Значит:\ \]
\[два\ угла\ при\ основании\ также\ \]
\[равны\ 60{^\circ};\]
\[\mathrm{\Delta}MNK - равносторонний.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
\[\boxed{\mathbf{861.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
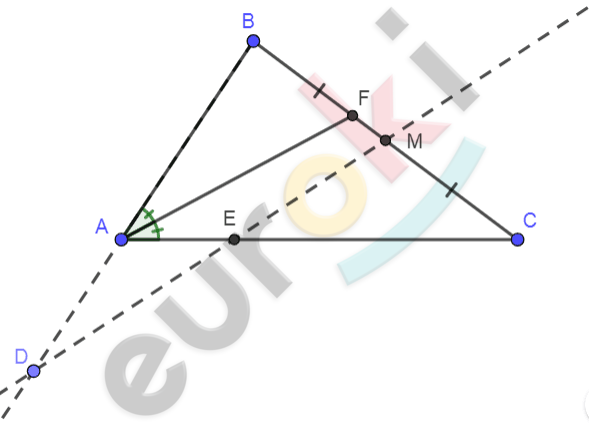
\[\mathrm{\Delta}ABC\ \left( \text{AB} \neq \text{AC} \right);\]
\[M \in BC;BM = MC;\]
\[AF - биссектриса\ \angle A;\]
\[MD \parallel AF;D \in AB;\]
\[F = MD \cap AC.\]
\[\mathbf{Доказать:}\]
\[BD = CE.\]
\[\mathbf{Доказательство.}\]
\[1)\ \mathrm{\Delta}DAE - равнобедренный,\ \]
\[с\ основанием\ DE:\]
\[MD \parallel AF \Longrightarrow \angle ADE = \angle BAF =\]
\[= \angle\frac{A}{2};\]
\[\angle DAE = 180{^\circ} - \angle A \Longrightarrow \ \]
\[\Longrightarrow \angle AED =\]
\[= 180 - \left( 180 - \angle A + \angle\frac{A}{2} \right) =\]
\[= \angle\frac{A}{2}.\]
\[Следовательно:AD = AE.\]
\[2)\ Пусть\ BM = MC = d;\ \ \]
\[FM = f:\]
\[MD \parallel AF;\ \ \angle B - общий;\ \ \]
\[\mathrm{\Delta}ABF\sim\mathrm{\Delta}DMB;\]
\[k_{1} = \frac{\text{BA}}{\text{BD}} = \frac{\text{BF}}{\text{BM}} = \frac{d - f}{d}\text{.\ }\]
\[Получаем:\]
\[AD = BD - BA = \left( 1 - \frac{d - f}{d} \right) =\]
\[= \frac{f}{d}\text{BD.}\]
\[3)\ MD \parallel AF;\ \ \angle B - общий \Longrightarrow\]
\[\Longrightarrow \mathrm{\Delta}MCE\sim\mathrm{\Delta}FCA;\]
\[k_{2} = \frac{\text{CE}}{\text{CA}} = \frac{\text{CM}}{\text{CF}} = \frac{d}{d + f}\text{.\ }\]
\[Отсюда:\]
\[AE = CA - CE =\]
\[= \left( \frac{d + f}{d} - 1 \right) \bullet CE = \frac{f}{d}\text{CE.}\]
\[4)Получаем:\]
\[AD = AE;\ \]
\[\frac{f}{d}BD = \frac{f}{d}CE;\ \ \]
\[BD = CE.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
