Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 844
Задание 844
\[\boxed{\mathbf{844.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - прямоугольник;\]
\[MB = a;\ \ MC = b;\]
\[MD = c.\]
\[\mathbf{Найти:}\]
\[MA - ?\]
\[\mathbf{Решение.}\]
\[1)\ Проведем\ через\ ( \bullet )\text{M\ }\]
\[прямые\ EF \parallel AD;\ \ GH \parallel AB.\]
\[2)\ Пусть\ MA = x;\ \ \]
\[AE = HM = FD = m;\ \]
\[EB = MG = FC = n;\ \ \]
\[BG = EM = AH = p;\]
\[GC = MF = HD = q.\]
\[3)\ По\ теореме\ Пифагора:\]
\[a^{2} = n^{2} + p^{2};\]
\[b^{2} = n^{2} + q^{2}.\]
\[Получаем:\]
\[a^{2} + c^{2} = n^{2} + p^{2} + m^{2} + q^{2} =\]
\[= x^{2} + b^{2};\]
\[c^{2} = m^{2} + q^{2};\]
\[x^{2} = m^{2} + p^{2}.\]
\[4)\ x^{2} = a^{2} - b^{2} + c^{2}\]
\[x = \sqrt{a^{2} - b^{2} + c^{2}}.\]
\[Ответ:\ \sqrt{a^{2} - b^{2} + c^{2}}.\]
\[\boxed{\mathbf{844.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
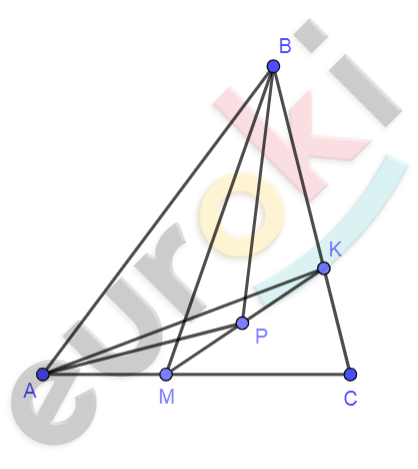
\[\mathrm{\Delta}ABC;\]
\[M \in AC;K \in BC;\]
\[P \in MK;\ \]
\[\frac{\text{AM}}{\text{MC}} = \frac{\text{CK}}{\text{KB}} = \frac{\text{MP}}{\text{PK}};\]
\[S_{\text{AMP}} = S_{1};\]
\[S_{\text{BKP}} = S_{2}.\]
\[\mathbf{Найти:}\]
\[S_{\text{ABC}} - ?\]
\[\mathbf{Решение.}\]
\[1)\ Допустим:\ \ \frac{\text{AM}}{\text{MC}} = \frac{\text{CK}}{\text{KB}} =\]
\[= \frac{\text{MP}}{\text{PK}} = k.\ \]
\[Тогда:\]
\[\frac{S_{\text{AMP}}}{S_{\text{APK}}} = \frac{\text{MP}}{\text{PK}} = k = \frac{S_{1}}{S_{\text{APK}}}\]
\[S_{\text{APK}} = \frac{S_{1}}{k};\]
\[S_{\text{AMK}} = S_{\text{AMP}} + S_{\text{APK}} =\]
\[= \left( 1 + \frac{1}{k} \right) \bullet S_{1}.\]
\[\frac{S_{\text{KAM}}}{S_{\text{KMC}}} = \frac{\text{AM}}{\text{MC}} = k = \frac{\left( 1 + \frac{1}{k} \right) \bullet S_{1}}{S_{\text{KMC}}}\]
\[S_{\text{KMC}} = \frac{\left( 1 + \frac{1}{k} \right) \bullet S_{1}}{k} =\]
\[= \frac{(k + 1)}{k^{2}} \bullet S_{1}.\]
\[Получаем:\]
\[S_{\text{ACK}} = S_{\text{KAM}} + S_{\text{KMC}} =\]
\[= \frac{(k + 1)}{k^{2}} \bullet S_{1} + \frac{(k + 1)}{k^{2}} \bullet S_{1} =\]
\[= \frac{(k + 1)^{2}}{k} \bullet S_{1}.\]
\[Значит:\]
\[\frac{S_{\text{ACK}}}{S_{\text{AKB}}} = \frac{\text{CK}}{\text{KB}} = k = \frac{(k + 1)^{2} \bullet S_{1}}{S_{\text{AKB}}}\]
\[S_{\text{AKB}} = \frac{1}{k} \bullet \left( \frac{k + 1}{k} \right)^{2} \bullet S_{1}\]
\[S_{\text{ABC}} = S_{\text{ACK}} + S_{\text{AKB}} =\]
\[= \frac{(k + 1)^{3}}{k} \bullet S_{1}.\]
\[2)\ \frac{S_{\text{BMP}}}{S_{\text{BPK}}} = \frac{\text{MP}}{\text{PK}} = k = \frac{S_{\text{BMP}}}{S_{2}}\]
\[S_{\text{BMP}} = kS_{2}\]
\[S_{\text{BMK}} = S_{\text{BMP}} + S_{\text{BPK}} =\]
\[= (k + 1) \bullet S_{2}.\]
\[\frac{S_{\text{MCK}}}{S_{\text{MKB}}} = \frac{\text{CK}}{\text{KB}} = k = \frac{S_{\text{MCK}}}{(k + 1)S_{2}}\]
\[S_{\text{MCK}} = k(k + 1)S_{2}\]
\[S_{\text{MCB}} = S_{\text{MCK}} + S_{\text{MKB}} =\]
\[= (k + 1)^{2}S_{2}.\]
\[\frac{S_{\text{BAM}}}{S_{\text{BMC}}} = \frac{\text{AM}}{\text{MC}} = k = \frac{S_{\text{BAM}}}{(k + 1)^{2}S_{2}}\]
\[S_{\text{BAM}} = k \bullet (k + 1)^{2} \bullet S_{2}\]
\[S_{\text{ABC}} = S_{\text{BAM}} + S_{\text{BMC}} =\]
\[= (k + 1)^{3} \bullet S_{2}.\]
\[3)\ Получаем:\]
\[\frac{(k + 1)^{3}}{k} \bullet S_{1} = (k + 1)^{3} \bullet S_{2}\]
\[k^{3} = \frac{S_{1}}{S_{2}}\]
\[k = \sqrt[3]{\frac{S_{1}}{S_{2}}}.\]
\[4)\ S_{\text{ABC}} = (k + 1)^{3} \bullet S_{2} =\]
\[= \left( \sqrt[3]{\frac{S_{1}}{S_{2}}} + 1 \right)^{3} \bullet S_{2} =\]
\[= \frac{\left( \sqrt[3]{S_{1}} + \sqrt[3]{S_{2}} \right)^{3}}{S_{2}} \bullet S_{2} =\]
\[= \left( \sqrt[3]{S_{1}} + \sqrt[3]{S_{2}} \right)^{3}.\]
\[Ответ:S_{\text{ABC}} = \left( \sqrt[3]{S_{1}} + \sqrt[3]{S_{2}} \right)^{3}.\]
