Решебник по геометрии 7 класс Атанасян ФГОС Задание 827

 

\[\boxed{\mathbf{827.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунки\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[a > b;\]

\[d - отрезки.\]

\[\mathbf{Построить:}\]

\[равнобедренную\ \]

\[трапецию,\ где\]

\[AD \parallel BC;AB = CD;\]

\[AD = a;BC = b;\]

\[AC = BD = d.\]

\[\mathbf{Решение.}\]

\[1)\ Построим\ произвольную\ \]

\[прямую\ f\ и\ поставим\ на\ ней\ \]

\[точку\ A.\]

\[2)\ Отложим\ отрезок\ AD = a;\]

\[DI = b.\]

\[3)\ Построим\ окружность\ с\ \]

\[центром\ A(A;d)\ и\ окружность\ \]

\[с\ центром\ I(I;d).\]

\[Радиусы\ окружностей\ равны\ \]

\[диагоналям\ трапеции.\]

\[4)\ Поставим\ точку\ \ C\ в\ месте\ \]

\[пересечения\ окружностей\ в\ \]

\[верхней\ полуплоскости.\]

\[5)\ Через\ ( \bullet )\text{D\ }\ проведем\ \]

\[прямую\ k,\ параллельную\ CI;\]

\[через\ ( \bullet )Cпроведем\ прямую\ h,\ \]

\[параллельную\ AD.\]

\[6)\ ( \bullet )\text{B\ \ }будет\ точкой\ \]

\[пересечения\ этих\ прямых.\]

\[ABCD - искомая\ трапеция.\]

\[\boxed{\mathbf{827.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Дано:}\]

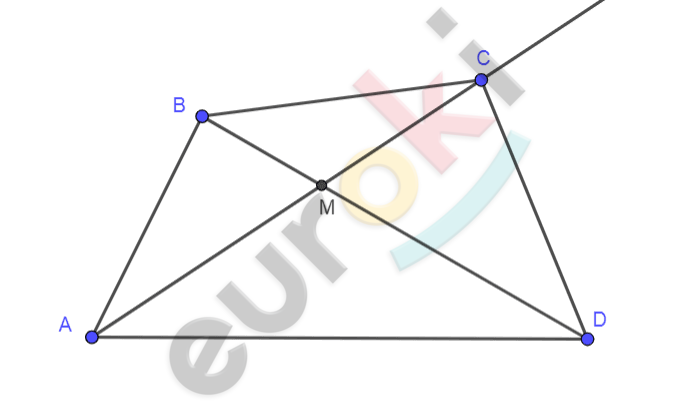
\(ABCD - выпуклый\)

\[четырехугольник.\]

\[\mathbf{Доказать:}\]

\[существует\ точка\]

\[M = \left| \text{AC} \right| \cap \left| \text{BD} \right|.\]

\[\mathbf{Доказательство.}\]

\[1)\ Четырехугольник\ \]

\[ABCD - выпуклый:\]

\[точки\ \text{C\ }и\ \text{D\ }лежат\ по\ одну\ \]

\[сторону\ от\ прямой\ AB;\]

\[точки\ \text{C\ }и\ \text{B\ }лежат\ по\ одну\ \]

\[сторону\ от\ прямой\ \text{AD.}\]

\[2)\ Следовательно:\]

\[Получаем:\]

\[существует\ точка\ \]

\[M = \left| \text{AC} \right| \cap \left| \text{BD} \right|.\]

\[3)\ Рассмотрим\ прямые\ \text{BA\ }и\ \]

\[\text{BC.\ }\]

\[Аналогично\ пункту\ второму\ \]

\[делаем\ вывод:\]

\[M = \left| \text{BD} \right| \cap \left| \text{AC} \right|.\]

\[Таким\ образом,\ точка\ M\ \]

\[не\ только\ лежит\ на\ луче,но\ \]

\[и\ \ является\ точкой\ \]

\[пересечения\ отрезков.\]

\[Что\ и\ требовалось\ доказать.\]