Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 826
Задание 826
\[\boxed{\mathbf{826.}\mathbf{ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}\text{ABC};\]
\[\text{BCDE};\text{ACTM};\]
\[\text{BAHK} - квадраты;\]
\[TCPQ;\]
\[EBKP - параллелограммы.\]
\[\mathbf{Доказать:}\]
\[\mathrm{\Delta}APQ - прямоугольный\ и\ \]
\[равнобедренный.\]
\[\mathbf{Доказательство.}\]
\[1)\ Допустим:\]
\[AB = c;BC = a;\ \]
\[\angle A = \alpha;\ \angle B = \beta.\]
\[2)\ Рассмотрим\ треугольники\ \]
\[ABC\ и\ \text{QCD}:\]
\[AC = TC = QD = b;\]
\[BC = CD = a;\]
\[\angle EDQ = \angle BCT = \angle C + 90{^\circ};\]
\[то\ \angle CDQ = \angle C.\]
\[По\ первому\ признаку\ \]
\[равенства\ \mathrm{\Delta}:\]
\[\mathrm{\Delta}ABC = \mathrm{\Delta}QCD;\ \]
\[CQ = c;\ \ \]
\[\angle ACQ =\]
\[= 360 - 90 - (\angle C + \angle B) =\]
\[= 90{^\circ} + \alpha.\]
\[3)\ Рассмотрим\ треугольники\ \]
\[\text{ABC\ }и\ PEB:\]
\[AB = KB = PE = c;\]
\[BC = EB = a;\]
\[\angle PEB = 180{^\circ} - \angle KBE =\]
\[= 180{^\circ} - (360{^\circ} - 290{^\circ} - \angle B) =\]
\[= \angle B.\]
\[По\ первому\ признаку\ \]
\[равенства\ треугольников:\]
\[\mathrm{\Delta}ABC = \mathrm{\Delta}PEB;\]
\[PB = b;\]
\[\angle PBA =\]
\[= 360{^\circ} - 90{^\circ} - (\angle C + \angle B) =\]
\[= 90{^\circ} + \alpha.\]
\[4)\ Рассмотрим\ треугольники\ \]
\[\text{PBA}\ и\ ACQ:\]
\[\angle PBA = \angle ACQ = 90{^\circ} + \alpha;\]
\[BA = CQ = c;\]
\[PB = AC = b;\ \ \ \]
\[по\ первому\ признаку\ равенства\ \]
\[треугольников:\]
\[\mathrm{\Delta}PBA = \mathrm{\Delta}ACQ;\]
\[PA = AQ;\ \ \ \ \]
\[\mathrm{\Delta}APQ - равнобедренный,\ с\ \]
\[основанием\ \text{PQ.}\]
\[5)\ \angle PBA = \angle CAQ = \gamma;\]
\[\angle BAP = \angle CQA = \beta.\ \]
\[Сумма\ углов\ треугольника\ \]
\[равна:\]
\[\gamma + \delta + (90{^\circ} + \alpha) = 180{^\circ};\]
\[\gamma + \delta + \alpha = 90{^\circ}.\]
\[Угол\ при\ вешине\ \]
\[\mathrm{\Delta}APQ - прямой:\]
\[\angle PAQ = \angle BAP + \angle A + \angle CAQ =\]
\[= \delta + \alpha + \gamma = 90{^\circ}.\]
\[Следовательно:\]
\[\mathrm{\Delta}APQ - прямоугольный\ и\ \]
\[равнобедренный.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{826.еуроки - ответы\ на\ пятёрку}}\]
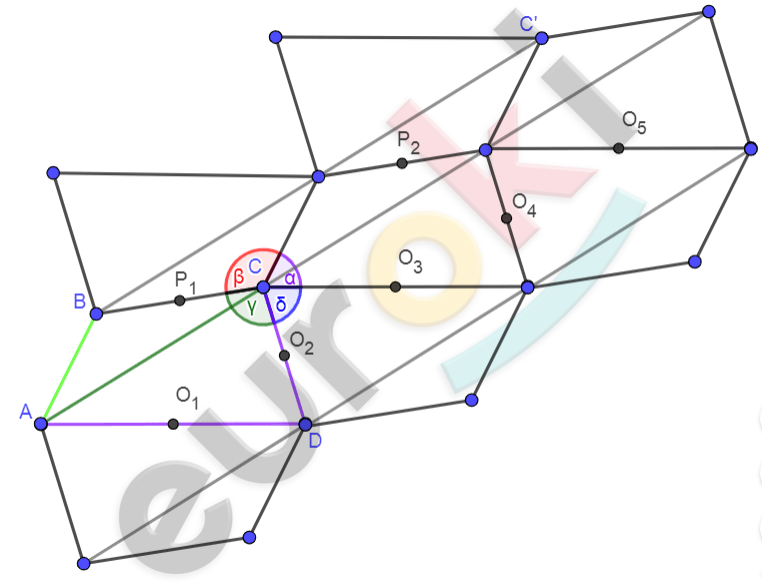
\[\mathbf{Дано:}\]
\(ABCD - выпуклый\)
\[четырехугольник.\]
\[\mathbf{Доказать:}\]
\(с\ помощью\ ABCD\) \(можно\ \)
\[замостить\ любую\ часть\ \]
\[плоскости.\]
\[\mathbf{Доказательство.}\]
\[Любую\ плоскость\ можно\ \]
\[замостить\ треугольниками,\ из\ \]
\[которых\ легко\ построить\ \]
\[параллелограммы.\ \ \]
\[Из\ последних\ же\ можно\ \]
\[сделать\ полосы.\ \]
\[Значит,\ если\ разделить\ \]
\[данный\ четырехугольник\ \]
\[на\ треугольники,\ то\ сможем\ \]
\[сделать\ полосы.\]
\[1)\ К\ стороне\ \text{AD\ }прикладываем\ \]
\[следующую\ плитку\ паркета\ \]
\[\left( стороной\ A_{1}D_{1} \right).\]
\[Получится\ \ отображение\ \]
\[относительно\ стороны\ \text{AD},\]
\[\ а\ ( \bullet )O_{1}\ будет\ \ центром\ \]
\[симметрии.\ \]
\[3)\ Повторяем\ эту\ операцию\ \]
\[для\ стороны\ \text{CD},\ затем\ \]
\[продолжаем\ далее.\ \]
\[4)\ В\ итоге\ у\ нас\ получится\ \]
\[полоса\ из\ треугольников,\ \]
\[равных\ \mathrm{\Delta}ACD;а\ зубцы\ будут\ \]
\[равны\ \mathrm{\Delta}\text{ABC.}\ \]
\[5)\ Продолжаем\ покрывать\ \]
\[пол.\ Выбираем\ центром\ \]
\[симметрии\ точку\ P_{1}\ \]
\[\left( середина\ стороны\ \text{BC} \right);\ \]
\[повторяем\ все\ шаги\ заново.\ \]
\[В\ итоге\ опять\ получится\ \]
\[полоса\ из\ треугольников,\ \]
\[равных\ \mathrm{\Delta}ABC.\]
\[6)\ Вывод:\]
\[за\ счет\ составляющих\ \]
\[четырехугольник\ ABCD\ \]
\[треугольников\ образуются\ \]
\[полосы,\ которые\ можно\ \]
\[использовать\ для\ покрытия\ \]
\[плоскости.\]
\[7)\ Выберем\ точку\ \text{C\ }на\ \]
\[рисунке\ и\ рассмотрим\ стык\ \]
\[из\ четырех\ плиток.\ \]
\[Так\ как\ плитки\ примыкают\ \]
\[друг\ к\ другу\ углами:\]
\[\angle A = \alpha;\ \ \angle B = \beta;\ \angle C = \gamma;\]
\[\ \ \angle D = \delta;\ \]
\[сумма\ которых\ равна\ 360{^\circ},\ то\ \]
\[зазоров\ не\ будет.\ \ \]
\[Значит,\ любая\ часть\ плоскости\ \]
\[будет\ покрыта\ полностью.\]
\[Что\ и\ требовалось\ доказать.\]
