Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 815
Задание 815
\[\boxed{\mathbf{815.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунки\ по\ условию\mathbf{\ задачи:}\]
\[\mathbf{Дано:}\]
\[ABCD - четырехугольник.\]
\[\mathbf{Доказать:}\]
\[точки\ \text{B\ }и\ \text{D\ }лежат\]
\(по\ разные\ стороны\) \(от\ \text{AC}.\)
\[\mathbf{Доказательство.}\]
\[1)\ Допустим,\ что\ \]
\[четырехугольник\ ABCD -\]
\[выпуклый:\ точки\ \text{C\ }и\ \text{D\ }будут\ \]
\[лежать\ по\ одну\ сторону\ от\ \]
\[прямой\ \text{AB};а\ точки\ \text{C\ }и\ \text{B\ }по\ \]
\[одну\ сторону\ от\ прямой\ \text{AD}.\]
\[Следовательно:\ \]
\[точка\ \text{C\ }находится\ внутри\ \]
\[\angle BAD;\]
\[а\ точки\ \text{B\ }и\ \text{D\ }лежат\ по\ разные\ \]
\[стороны\ от\ прямой\ \text{AC}.\]
\[\ 2)\ Допустим,\ что\ \]
\[четырехугольник\ ABCD - не\ \]
\[выпуклый\ и\ прямая\ \text{BC\ }\]
\[перескает\ его\ сторону\ \text{AD}:\]
\[\ E = \left| \text{BC} \right| \cap \left| \text{AD} \right|\text{.\ }\]
\[Следовательно:\ \]
\[точка\ C \in отрезку\ \text{BE\ }и\ лежит\ \]
\[внутри\ угла\ \text{BAE};\]
\[точка\ \text{C\ }находится\ внутри\]
\[угла\ \text{BAD}.\]
\[Значит:\ \]
\[\text{B\ }и\ \text{D\ }лежат\ по\ разные\ \]
\[стороны\ от\ \text{AC.}\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
\[\boxed{\mathbf{815.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
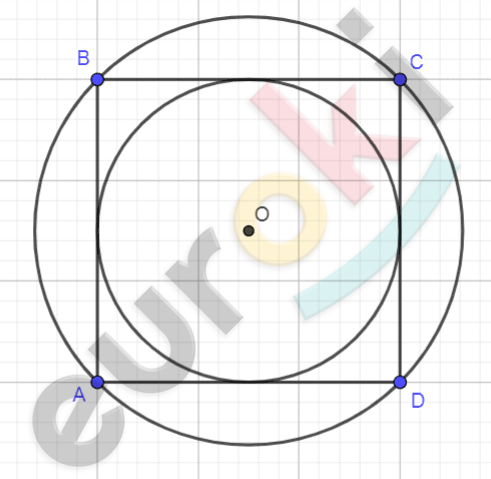
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - параллелограмм.\]
\[\mathbf{Доказать:}\]
\[ABCD - квадрат.\]
\[\mathbf{Доказательство.}\]
\[1)\ ABCD - вписанный:\]
\[\angle C + \angle A = 180{^\circ}\ и\ \angle D = \angle B =\]
\[= 90{^\circ}.\]
\[Отсюда:\]
\[\angle A = \angle C = \angle B = \angle D = 90{^\circ}.\]
\[2)\ ABCD - описанный:\]
\[CD + AB = AD + BC\ и\ BC =\]
\[= AD;\ \]
\[AB = CD.\]
\[Отсюда:\]
\[AB = BC = CB = AD.\]
\[3)\ Следовательно:\]
\[ABCD - квадрат.\]
\[Что\ и\ требовалось\ доказать.\]
