Решебник по геометрии 7 класс Атанасян ФГОС Задание 764

 

\[\boxed{\mathbf{764.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[\textbf{а)}\ \left( \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}} - \overrightarrow{\text{MC}} \right) + \left( \overrightarrow{\text{MD}} - \overrightarrow{\text{KD}} \right) =\]

\[= \left( \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}} + \overrightarrow{\text{CM}} \right) + \left( \overrightarrow{\text{MD}} + \overrightarrow{\text{DK}} \right) =\]

\[= \overrightarrow{\text{AM}} + \overrightarrow{\text{MK}} = \overrightarrow{\text{AK}}.\]

\[\textbf{б)}\ \left( \overrightarrow{\text{CB}} + \overrightarrow{\text{AC}} + \overrightarrow{\text{BD}} \right) - \left( \overrightarrow{\text{MK}} + \overrightarrow{\text{KD}} \right) =\]

\[= \left( \overrightarrow{\text{AC}} + \overrightarrow{\text{CB}} + \overrightarrow{\text{BD}} \right) - \overrightarrow{\text{MD}} =\]

\[= \overrightarrow{\text{AD}} + \overrightarrow{\text{DM}} = \overrightarrow{\text{AM}}.\]

\[\boxed{\mathbf{764.еуроки - ответы\ на\ пятёрку}}\]

\[1)\ Рисунок\ по\ условию\ задачи:\]

\[\mathbf{а)}\]

\(\mathbf{\ }\)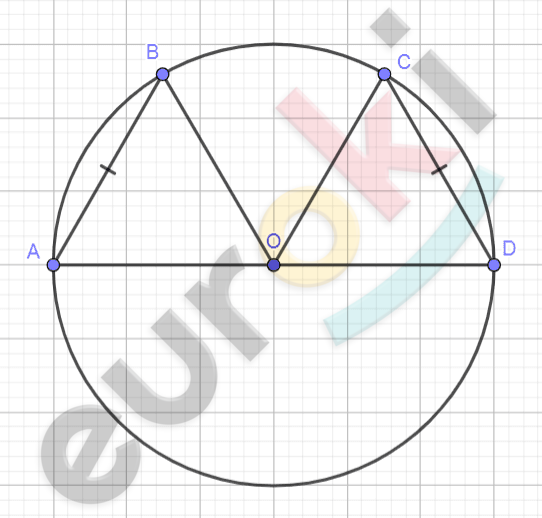

\[\mathbf{б)\ }\]

\[\mathbf{Дано:}\]

\[окружность\ (O,\ R);\ \]

\[AB = CD;\]

\[\angle AOB = 112{^\circ}\]

\[\mathbf{Доказать:}\]

\[\cup AB = \cup CD.\]

\[Найти:\]

\[\cup CD - ?\ \]

\[\cup CBD - ?\]

\[\mathbf{Решение.}\]

\[1)\ \mathrm{\Delta}ABO = \mathrm{\Delta}OCD - по\ трем\ \]

\[сторонам:\]

\[BO = AO = OC = OD = r;\]

\[AB = CD\ (по\ условию).\]

\[Отсюда:\]

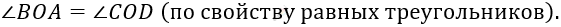
\[2)\ \angle BOA = \cup AB\ \]

\[(как\ центральный);\ \]

\[\angle COD = \cup CD\ \]

\[(как\ центральный);\]

\[\ \angle BOA = \angle COD.\]

\[Следовательно:\ \]

\[\cup AB = \cup CD.\]

\[Что\ и\ требовалось\ доказать.\]

\[3)\ \angle BOA = \angle COD = 112{^\circ}\ \]

\[(как\ вертикальные):\]

\[\angle COD = \cup CD = 112{^\circ}\ \]

\[(как\ центральный).\]

\[4)\ \cup CBD = 360{^\circ} - 112{^\circ} =\]

\[= 248{^\circ}.\]

\[Ответ:\ \cup CD = 112{^\circ}\ и\ \]

\(\cup CBD = 248{^\circ}.\)