Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 747
Задание 747
\[\boxed{\mathbf{747.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[\textbf{а)}\ Параллелограмм\ MNPQ.\]
\[Коллинеарные:\ \]
\[\overrightarrow{\text{NP}}\ и\ \overrightarrow{\text{MQ}};\ \overrightarrow{\text{MN}}\ и\ \overrightarrow{\text{PQ}};\ \overrightarrow{\text{PN}}\ и\ \overrightarrow{\text{QM}};\ \]
\[\overrightarrow{\text{MN}}\ и\ \overrightarrow{\text{QP}};\ \overrightarrow{\text{NP}}\ и\ \overrightarrow{\text{QM}};\ \]
\[\overrightarrow{\text{PN}}\ и\ \overrightarrow{\text{MQ}};\ \overrightarrow{\text{NM}}\ и\ \overrightarrow{\text{PQ}};\ \overrightarrow{\text{NM}}\ и\ \overrightarrow{\text{QP}}.\]
\[Сонаправленные:\ \]
\[\overrightarrow{\text{NP}}\ и\ \overrightarrow{\text{MQ}};\ \overrightarrow{\text{PN}}\ и\ \overrightarrow{\text{QM}};\ \overrightarrow{\text{NM}}\ и\ \overrightarrow{\text{PQ}};\ \]
\[\overrightarrow{\text{MN}}\ и\ \overrightarrow{\text{QP}}\text{.\ }\]
\[Противоположно\ \]
\[направленные:\ \ \]
\[\overrightarrow{\text{NP}}\ и\ \overrightarrow{\text{QM}};\ \overrightarrow{\text{PN}}\ и\ \overrightarrow{\text{MQ}};\ \overrightarrow{\text{NM}}\ и\ \overrightarrow{\text{QP}};\ \]
\[\overrightarrow{\text{MN}}\ и\ \overrightarrow{\text{PQ}}\text{.\ \ \ }\]
\[\textbf{б)}\ Трапеция\ ABCD\ с\ \]
\[основаниями\ \text{AD\ }и\ \text{BC.}\]
\[Коллинеарные:\ \]
\[\overrightarrow{\text{BC}}\ и\ \overrightarrow{\text{AD}};\ \overrightarrow{\text{BC}}\ и\ \overrightarrow{\text{DA}};\ \overrightarrow{\text{CB}}\ и\ \overrightarrow{\text{DA}};\ \]
\[\overrightarrow{\text{CB}}\ и\ \overrightarrow{\text{AD}}.\]
\[Сонаправленные:\ \]
\[\overrightarrow{\text{BC}}\ и\ \overrightarrow{\text{AD}};\ \overrightarrow{\text{CB}}\ и\ \overrightarrow{\text{DA}}\text{.\ }\]
\[Противоположно\ \]
\[направленные:\ \]
\[\overrightarrow{\text{BC}}\ и\ \overrightarrow{\text{DA}};\ \overrightarrow{\text{CB}}\ и\ \overrightarrow{\text{AD}}.\]
\[\textbf{в)}\ Треугольник\ FGH.\]
\[Нет\ коллинеарных\ векторов.\]
\[\boxed{\mathbf{747.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
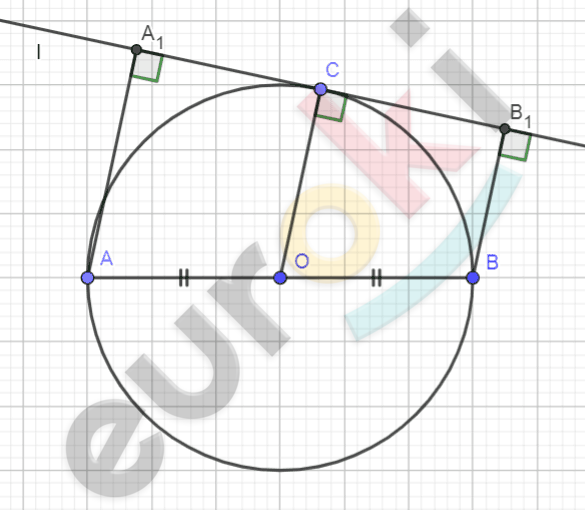
\[\mathbf{Дано:}\]
\[окружность\ (O,\ R);\ \]
\[AB = 2R;\]
\[C \in l - касательная;\]
\[AA_{1}\bot l;\]
\[BB_{1}\bot l.\]
\[\mathbf{Доказать:}\]
\[A_{1}C = CB_{1}.\]
\[\mathbf{Доказательство.}\]
\[1)\ AA_{1}\bot l\ и\ BB_{1}\bot l:\]
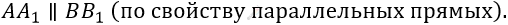
\[Следовательно:\ \]
\[ABCD - \ прямоугольная\ \]
\[трапеция\ (по\ определению).\]
\[2)\ OC\bot l:\]
\[AA_{1} \parallel OC \parallel BB_{1};\ \]
\[OA = BO;\ \]
\[O \in AB.\]
\[По\ теореме\ Фалеса:\]
\[OC - средняя\ линия\ \]
\[трапеции \Longrightarrow \ A_{1}C = CB_{1}.\]
\[Что\ и\ требовалось\ доказать.\]
