Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 746
Задание 746
\[\boxed{\mathbf{746.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - прямоугольная\ \]
\[трапеция;\]
\[\angle A = 90{^\circ};\]
\[AD = 12\ см;\]
\[AB = 5\ см;\]
\[\angle D = 45{^\circ}.\]
\[\mathbf{Найти:}\]
\[\left| \overrightarrow{\text{BD}} \right|;\left| \overrightarrow{\text{CD}} \right|;\left| \overrightarrow{\text{AC}} \right| - ?\]
\[\mathbf{Решение.}\]
\[1)\ По\ теореме\ Пифагора:\]
\[BD = \sqrt{AB^{2} + AD^{2}} =\]
\[= \sqrt{25 + 144} = \sqrt{169} = 13\ см.\]
\[\left| \overrightarrow{\text{BD}} \right| = 13\ см.\]
\[2)\ CH = BA =\]
\[= 5\ см\ (как\ высота).\]
\[3)\ \mathrm{\Delta}CHD - прямоугольный;\]
\[равнобедренный:\]
\[\angle CDH = 45{^\circ} \Longrightarrow \ \angle HCD = 45{^\circ}.\]
\[Отсюда:\ \]
\[CH = HD = 5\ см.\]
\[4)\ AH = AD - HD = 12 - 5 =\]
\[= 7\ см.\]
\[5)\ BC = AH = 7\ см.\]
\[6)\ По\ теореме\ Пифагора:\]
\[CD = \sqrt{CH^{2} + HD^{2}} =\]
\[= \sqrt{25 + 25} = \sqrt{50} = 5\sqrt{2}\ см;\]
\[\left| \overrightarrow{\text{CD}} \right| = 5\sqrt{2}\ см.\]
\[7)\ AC = \sqrt{AB^{2} + BC^{2}} =\]
\[= \sqrt{25 + 49} = \sqrt{74}\ см;\]
\[\left| \overrightarrow{\text{AC}} \right| = \sqrt{74}\ см.\]
\[\mathbf{Ответ:\ }\left| \overrightarrow{\text{BD}} \right| = 13\ см;\ \]
\[\left| \overrightarrow{\text{CD}} \right| = 5\sqrt{2}\ см;\ \left| \overrightarrow{\text{AC}} \right| = \sqrt{74}\ см.\]
\[\boxed{\mathbf{746.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
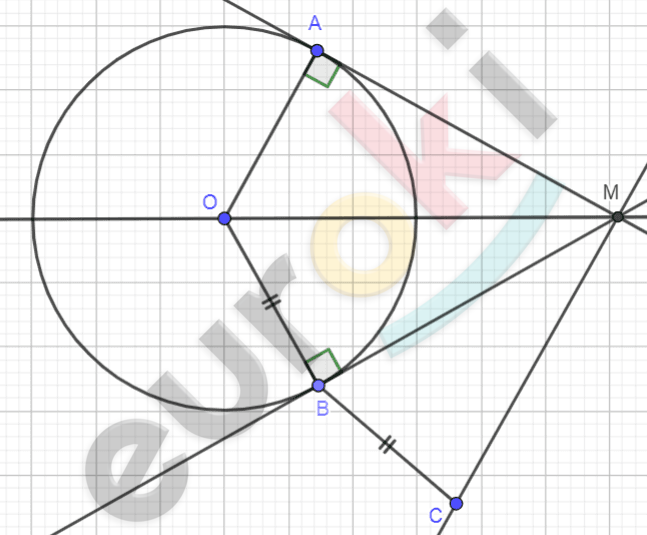
\[\mathbf{Дано:}\]
\[окружность\ (O,\ R);\ \]
\[\text{BM}\ и\ \text{AM} - касательные;\]
\[OB = BC.\]
\[\mathbf{Доказать:}\]
\[\angle AMC = 3\angle BMC.\]
\[\mathbf{Доказательство.}\]
\[1)\ \mathrm{\Delta}OMB = \mathrm{\Delta}CMB\ - по\ двум\ \]
\[катетам:\]
\[MB - общая\ сторона;\ \]
\[OB = BC\ (по\ условию).\]
\[Отсюда:\]
\[\angle OMB = \angle CMB.\]
\[2)\ \angle BMO = \angle AMO\ \]
\[(по\ свойству\ катетов).\]
\[3)\ \angle AMC =\]
\[= \angle AMO + \angle BMC + \angle OMB\]
\[\angle OMB = \angle CMB = \angle AMO\]
\[\ \angle AMC = 3\angle BMC.\]
\[Что\ и\ требовалось\ доказать.\]
